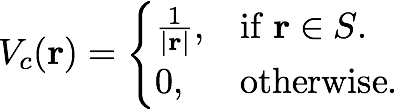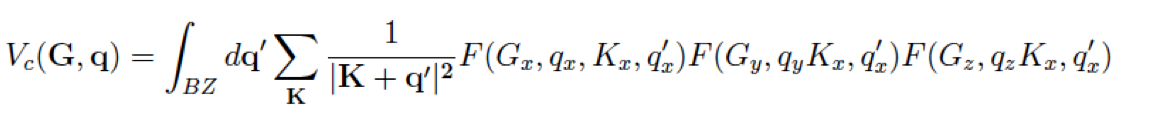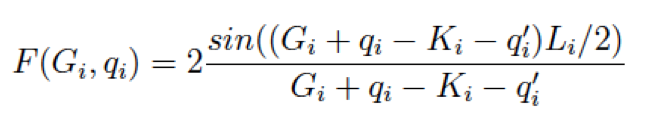How to treat low dimensional systems

In this tutorial you will learn (for a 2D material) how to:

• generate a coulomb potential with a box-like cutoff in the non-periodic direction
• visualize this coulomb potential
• use this cutoff in the HF, GW and BSE calculation
• analyze the difference with similar calculations without cutoff

Prerequisites

• Complete the Generating the Yambo databases tutorial
• SAVE folder for 2D hBN.
• yambo executable
• ypp executable
• Run Initialization

Generate the cutoff database (yambo -r)

To simulate an isolated nano-material a convergence with cell vacuum size is in principle required, like in the DFT runs.

The use of a truncated Coulomb potential allows to achieve faster convergence eliminating the interaction between the repeated images along the non-periodic direction (see i.e. D. Varsano et al Phys. Rev. B and .. )

In YAMBO you can use :

spherical cutoff (for 0D systems)
cylinder  cutoff (for 1D systems)
box-like  cutoff (for 0D, 1D and also 2D systems)

In this tutorial we learn how to use the box-like coulomb potential for a 2D system with non-periodic direction along z.

The Coulomb potential with a box-like cutoff is defined as

Then the FT component is

where

For a 2D-system with non period direction along z-axis we have

For a 2D system a box-like cutoff in the direction perperdicular to the sheet (in this case z) is applied. The used box size L_z = a_z (cell size in bohr) - 1 bohr = 32 bohr

Create the input file:

$ yambo -F 01_cut2D.in  -r

Open the input file 01_cut2D.in

Change the variables inside as:

RandQpts= 1000000          # [RIM] Number of random q-points in the BZ
RandGvec= 100        RL    # [RIM] Coulomb interaction RS components

CUTGeo= "box z"            # [CUT] Coulomb Cutoff geometry: box/cylinder/sphere X/Y/Z/XY..
% CUTBox
 0.00     | 0.00     | 32.0    |        # [CUT] [au] Box sides

Close the input file and run yambo

$ yambo -F 01_cut2D.in  -J 2D