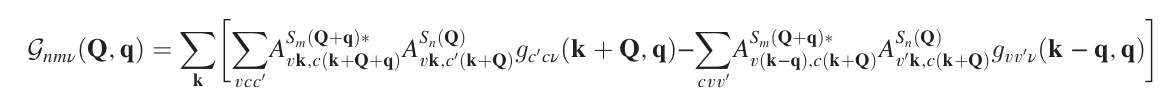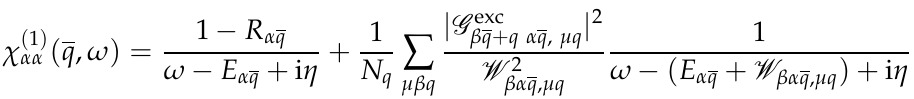Exciton-phonon coupling and luminescence: Difference between revisions
| Line 105: | Line 105: | ||
#DiagExcph # [EXCPH] Use only Diagonal Exciton-phonon matrix elements | #DiagExcph # [EXCPH] Use only Diagonal Exciton-phonon matrix elements | ||
% DmRngeXd | % DmRngeXd | ||
<span style="color:red"> 0. | <span style="color:red"> 0.0005000 | 0.0005000 | </span> eV # [Xd] Damping range | ||
notice that in this case <span style="color:red">[Xd] Damping range</span> is the broadening of the exciton-phonon self energy and it should be a very small value of the order of the phonon life-times about 0.5 meV.<ref>[https://arxiv.org/abs/1411.5628 First-principles calculations of phonon frequencies, lifetimes, and spectral functions from weak to strong anharmonicity: The example of palladium hydrides], L. Paulatto, et al. Phys. Rev. B '''91''', 054304 (2015) </ref> | notice that in this case <span style="color:red">[Xd] Damping range</span> is the broadening of the exciton-phonon self energy and it should be a very small value of the order of the phonon life-times about 0.5 meV.<ref>[https://arxiv.org/abs/1411.5628 First-principles calculations of phonon frequencies, lifetimes, and spectral functions from weak to strong anharmonicity: The example of palladium hydrides], L. Paulatto, et al. Phys. Rev. B '''91''', 054304 (2015) </ref> | ||
Revision as of 11:16, 24 February 2022
This tutorial works only with Yambo version > 6.x
The exciton-phonon part of Yambo does not support symmetries yet!!!
This an advanced tutorial, in order to calculate exciton-phonon coupling and phonon-assisted absorption/emission you need a deep knowledge of the theory and of the Yambo code.
In this tutorial we will calculate phonon-assisted absorption and luminescence including the scattering between exciton and phonon.[1][2][3]
We will consider as example bulk silicon. Notice that parameters of the present tutorial are not at convergence, but are just as a possible example.
The tutorial includes several steps and the calculations can be quite expensive.
Electron-phonon matrix elements
First of all we calculate electron-phonon matrix elements as explained in the section: Electron-phonon matrix elements but in the last passage of the tutorial we expand the electron-phonon matrix elements in all the Brillouin Zone. In order to do so, when we read the electron-phonon matrix elements from QE with the command ypp_ph -g g we turn on the flag GkkpExpand
gkkp # [R] gkkp databases gkkp_db # [R] GKKP database #GkkpReadBare # Read the bare gkkp DBsPATH= "../elph_dir/" # Path to the PW el-ph databases PHfreqF= "none" # PWscf format file containing the phonon frequencies PHmodeF= "none" # PWscf format file containing the phonon modes GkkpExpand # Expand the gkkp in the whole BZ #UseQindxB # Use qindx_B to expand gkkp (for testing purposes)
if everything worked fine in the log you will find:
.... <---> :: Uniform sampling :yes <---> :: Symmetry expanded :yes .....
Notice that in the calculation of the electron-phononn coupling you need a number of conduction bands as large as the one that will be used in the Bethe-Salpeter Equation.
Remove all symmetries
Now we remove all symmetries with the command ypp_ph -y
fixsyms # [R] Remove symmetries not consistent with an external perturbation
% Efield1
0.000000 | 0.000000 | 0.000000 | # First external Electric Field
%
% Efield2
0.000000 | 0.000000 | 0.000000 | # Additional external Electric Field
%
BField= 0.000000 T # [MAG] Magnetic field modulus
Bpsi= 0.000000 deg # [MAG] Magnetic field psi angle [degree]
Btheta= 0.000000 deg # [MAG] Magnetic field theta angle [degree]
RmAllSymm # Remove all symmetries
#RmTimeRev # Remove Time Reversal
#RmSpaceInv # Remove Spatial Inversion
#KeepKGrid # Do not expand the k-grid
the code will expand the electronic wave-function and copy the gkkp_expanded databases in the new folder.
BSE at finite momentum
Go in the folder without symmetries, run the setup, perform the GW calculation if required from your system,
and then run the BSE for all momentum q
as explained in the tutorials: BSE basic, BSE convergence, BSE for 2D.
Do not forget to turn on the flag WRbsWF to write the excitonic wave-functions.
Exciton-phonon matrix elements and optics
Now that you have the BSE for all momentum and the gkkp_expanded databases you can create the exciton-phonon matrix elements, according to the equation:
and calculate optical response as:
where Wβα,μq =Eβq − Eα + ωqμ ,for more details see Ref.[4]. Phonon-assisted optical response and exciton-phonon matrix elements can be calculated with the command: yambo_ph -excph o
excph # [R] Exction-phonon ExcGkkp # [R][EXCPH] Exciton-Phonon Matrix Elelements ExcPhOptics # [R][EXCPH] Exciton-Phonon Optics BoseTemp=-1.000000 eV # Bosonic Temperature % ELPhExcStates 1 | 2 | # [EXCPH] Incoming (external) exciton states % % ELPhExcSum 1 | 6 | # [EXCPH] Outgoing (virtual) exciton states % LoutPath= "none" # [EXCPH] Path of the outgoing L EXCTemp= 0.000000 eV # [EXCPH] Excitonic Temperature (for luminescence spectra) #DiagExcph # [EXCPH] Use only Diagonal Exciton-phonon matrix elements #DBGSigmaOnly # [EXCPH] Double-grid only for Sigma % EnRngeXd 0.00000 | 10.00000 | eV # [Xd] Energy range % % DmRngeXd 0.100000 | 0.100000 | eV # [Xd] Damping range % ETStpsXd= 100 # [Xd] Total Energy steps
where the ELPhExcStates state are the one responsible for the absorption and emission, the α indexes in the χαα and ELPhExcSum are the virtual exciton states that enter in the exciton-phonon scattering, namely the β index in the sum χαα. Running the code, Yambo calculates all the exciton-phonon matrix elements and the photon assisted absorption and emission spectra. The emission spectra is calculated using the Roosbroeck–Shockley (RS) relation[5], a Boltzman distribution for the excitonic occupation at temperature EXCTemp, for more detail see Refs.[4][2], other ways for excitonic occupations are possible, for a discussion see Ref.[1].
LoutPath is the path of the outgoing Bethe-Salpeter, in principle one can use two different kind of exciton for virtual and real exciton in above equation. If LoutPath='none' Yambo will read excitons in the same folder of the incoming ones, by default the SAVE folder.
If the flag DBGSigmaOnly is turned one the Double-Grid is used only for the denominator of the Xhi and not for the weight factors.
Exciton lifetimes
Using the exciton-phonon coupling it is possible also to calculate exciton life-time due to the scattering with phonon. The command yambo -excph l will generate the corresponding input:
excph # [R] Exction-phonon
ExcGkkp # [R][EXCPH] Exciton-Phonon Matrix Elelements
ExcPhLifeT # [R][EXCPH] Exciton-Phonon Life-Times
BoseTemp= 1.000000 eV # Bosonic Temperature
% ELPhExcStates
1 | 4 | # [EXCPH] Incoming (external) exciton states
%
% ELPhExcSum
1 | 8 | # [EXCPH] Outgoing (virtual) exciton states
%
LoutPath= "none" # [EXCPH] Path of the outgoing L
#DiagExcph # [EXCPH] Use only Diagonal Exciton-phonon matrix elements
% DmRngeXd
0.0005000 | 0.0005000 | eV # [Xd] Damping range
notice that in this case [Xd] Damping range is the broadening of the exciton-phonon self energy and it should be a very small value of the order of the phonon life-times about 0.5 meV.[6]
Convergence and double-grid
The exciton-phononn coupling code is compatible with the Double-Grid approach. You can generate a double grid for the phonon energies as explained in Double-grid method for the electron-phonon coupling and then the excitonic energies are interpolated using a smooth Fourier interpolation, see Ref.[7]. The best strategy to converge the spectra it is to chose a grid for the exciton-phonon matrix elements and then converge the double-grid, then repeat the calculation with a large exciton-phonon coupling grid and so on... similar to the electron-phonon case.
References
- ↑ 1.0 1.1 Theory of phonon-assisted luminescence in solids: Application to hexagonal boron nitride, E. Cannuccia, B. Monserrat and C. Attaccalite, Phys. Rev. B 99, 081109(R) (2019)
- ↑ 2.0 2.1 Exciton-Phonon Coupling in the Ultraviolet Absorption and Emission Spectra of Bulk Hexagonal Boron Nitride, F. Paleari et al. PRL 122, 187401(2019)
- ↑ Exciton-Phonon Interaction and Relaxation Times from First Principles, Hsiao-Yi Chen, Davide Sangalli, and Marco Bernardi, Phys. Rev. Lett. 125, 107401(2020)
- ↑ 4.0 4.1 First-principles approaches to the description of indirect absorption and luminescence spectroscopy: exciton-phonon coupling in hexagonal boron nitride, F. Paleari PhD thesis
- ↑ Photon-Radiative Recombination of Electrons and Holes in Germanium, W. van Roosbroeck and W. Shockley, Phys. Rev. 94, 1558 (1954)
- ↑ First-principles calculations of phonon frequencies, lifetimes, and spectral functions from weak to strong anharmonicity: The example of palladium hydrides, L. Paulatto, et al. Phys. Rev. B 91, 054304 (2015)
- ↑ Smooth Fourier interpolation of periodic functions, Warren E. Pickett, Henry Krakauer, and Philip B. Allen, Phys. Rev. B 38, 2721(1988)