Self-consistent GW on eigenvalues only: Difference between revisions
No edit summary |
No edit summary |
||
| Line 27: | Line 27: | ||
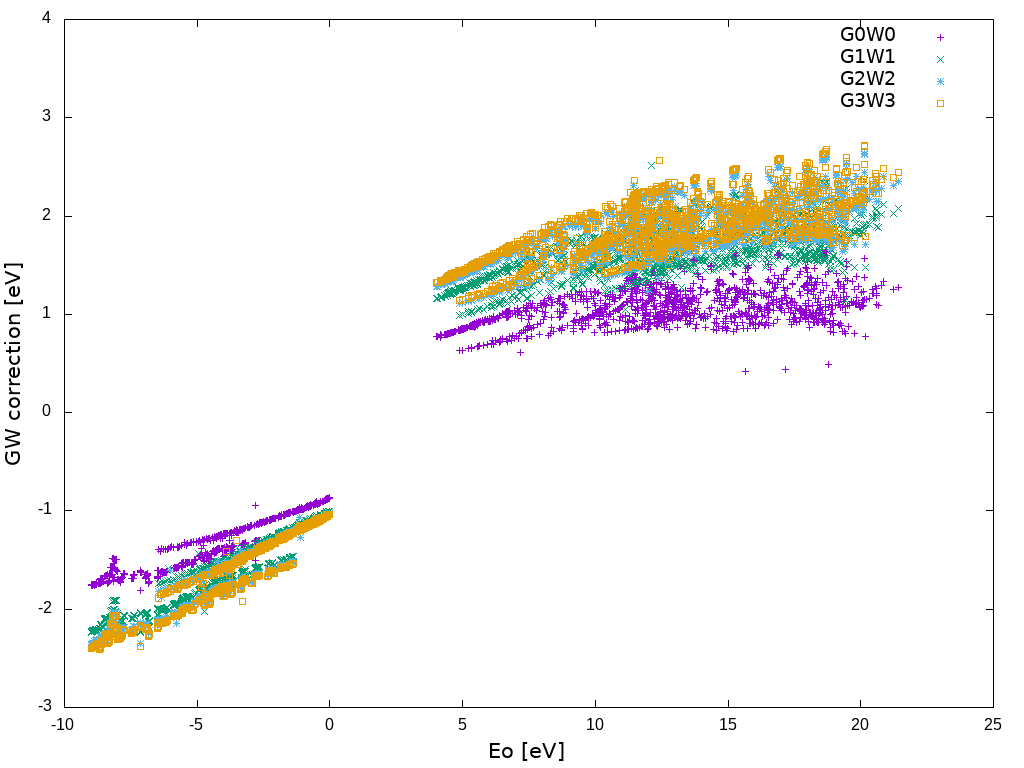
As example you can consider the results on hexgonal-Boron Nitride in ref.<ref>Artus L. et al. [https://doi.org/10.1002/adpr.202000101 Ellipsometry Study of Hexagonal Boron Nitride using Synchrotron Radiation: Transparency Window in the Far‐UVC]</ref> | As example you can consider the results on hexgonal-Boron Nitride in ref.<ref>Artus L. et al. [https://doi.org/10.1002/adpr.202000101 Ellipsometry Study of Hexagonal Boron Nitride using Synchrotron Radiation: Transparency Window in the Far‐UVC]</ref> | ||
[[File:Qp hbn.png|center|Self-consistent GW on eigenvalues]] | [[File:Qp hbn.png|center|400px| Self-consistent GW on eigenvalues]] | ||
Revision as of 21:28, 19 February 2021
In this tutorial you will learn how to perform self-consistent GW on eigenvalues only for G or both G and W (evGW). For molecules systems and also for many solids, the G0W0 approach often gives poor results. The main reason of this failure is that the DFT starting point with local or semi-local exchange correlation functionals give a too small gap compared with the experimental one, and a single shot GW is not able to correct this error. In order to overcome this problem a possible solution is to use as starting point a hybrid functional like PBE0, B3LYP,HSE etc.. or to perform a self-consistent GW. In general in self-consistent GW also the wave-function should be updated, but for many systems DFT wave-functions are already quite good and a self-consistency on eigenvalues only can be sufficient, for a discussion see for example ref.[1]
In this tutorial we will show how to perform self-consistent GW on the eigenvalues only with the Yambo code.
- Generate an input file for a G0W0 calculation as explained in the GW basics tutorial doing:
yambo -X p -g n -p p -V qp -F yambo_g0w0_input.in - run your first GW calculation doing:
yambo –F yambo_g0w0_input.in -J G0W0 - at the end of the run you will get a quasi-particle file o-G0W0.qp.
Now you can read this new quasi-particle band structure and perform another GW. - copy your gw input in a new file: cp yambo_g0w0_input.in yambo_g1w1_input.in
- modify the
yambo_g1w1_input.into force Yambo to read the previous quasi-particle corrections
GfnQPdb= "E < ./G0W0/ndb.QP"
and
XfnQPdb= "E < ./G0W0/ndb.QP" - repeat point 1) and 2) for the G1W1, G2W2, etc… until the differences between o-GnWn.qp and o-Gn+1Wn+1.qp are small enough.
Usually self-consistent GW converges in about 3/4 iterations. Notice that self-consistency on the eigenvalues can modify the energy level orders.
Moreover evGW removes large part of dependency of the GW results from the DFT functional.
If you want to perform self-consistency only on G and not on W comment the line:
#XfnQPdb= "E < ./GW0/ndb.QP"
Convergence issues: convergence parameters for the self-consisntet GW are the same of the standard GoWo calculation plus the bands range QPkrange employed for the self-consistency. You should perform some test with different band range and see if you converge to the same result. Do not use non-continuous bands/k-points range this could give wired results and the code does not check against this errors.
Internal and external self-consistency in Yambo: In Yamo there is another way to perform self-consisent GW, t
As example you can consider the results on hexgonal-Boron Nitride in ref.[2]