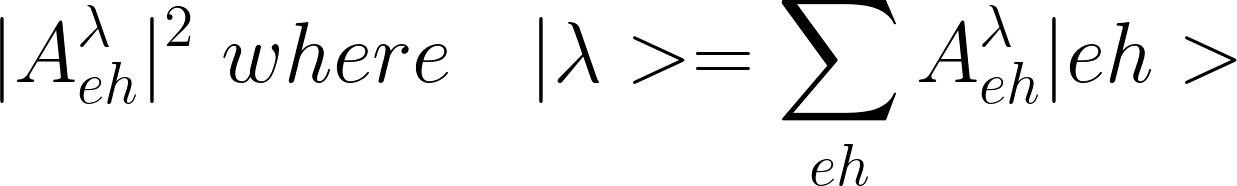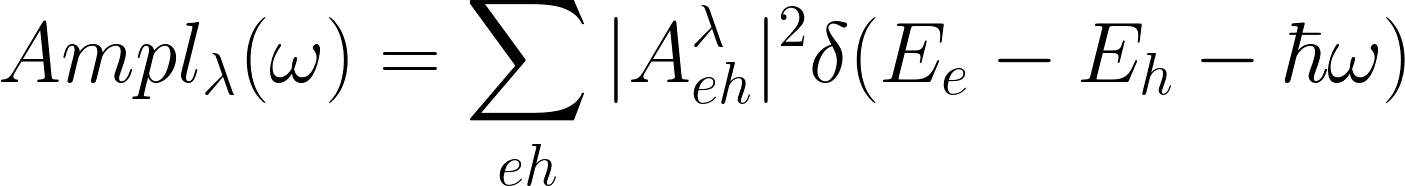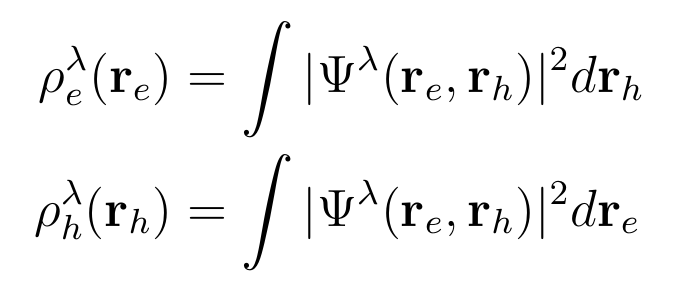How to analyse excitons

In this tutorial you will learn (for a 2D-hBN) how to:

• analyze a BSE optical spectrum in terms of excitonic eigenvectors and eigenvalues
• look at the spatial distribution of the exciton

Prerequisites

Previous modules

• You must have completed the How to treat low dimensional systems tutorial

You will need:

• ypp executable
• xcrysden executable
• gnuplot or xmgrace executable

YAMBO calculations

If you have completed the tutorials of 2D hBN you should have all the databases required to do this tutorial in your YAMBO_TUTORIALS/hBN-2D/SAVE and 2D_WR_WC (databases generated with RIM and cutoff) directories

$ ls ./SAVE
ndb.gops ndb.kindx ns.db1  ns.kb_pp_pwscf_fragment_1 ....
$ ls ./2D_WR_WC
ndb.BS_Q1_CPU_0	ndb.cutoff	ndb.dip_iR_and_P_fragment_1	ndb.pp_fragment_1 ...

Sort the excitonic eigenvalues

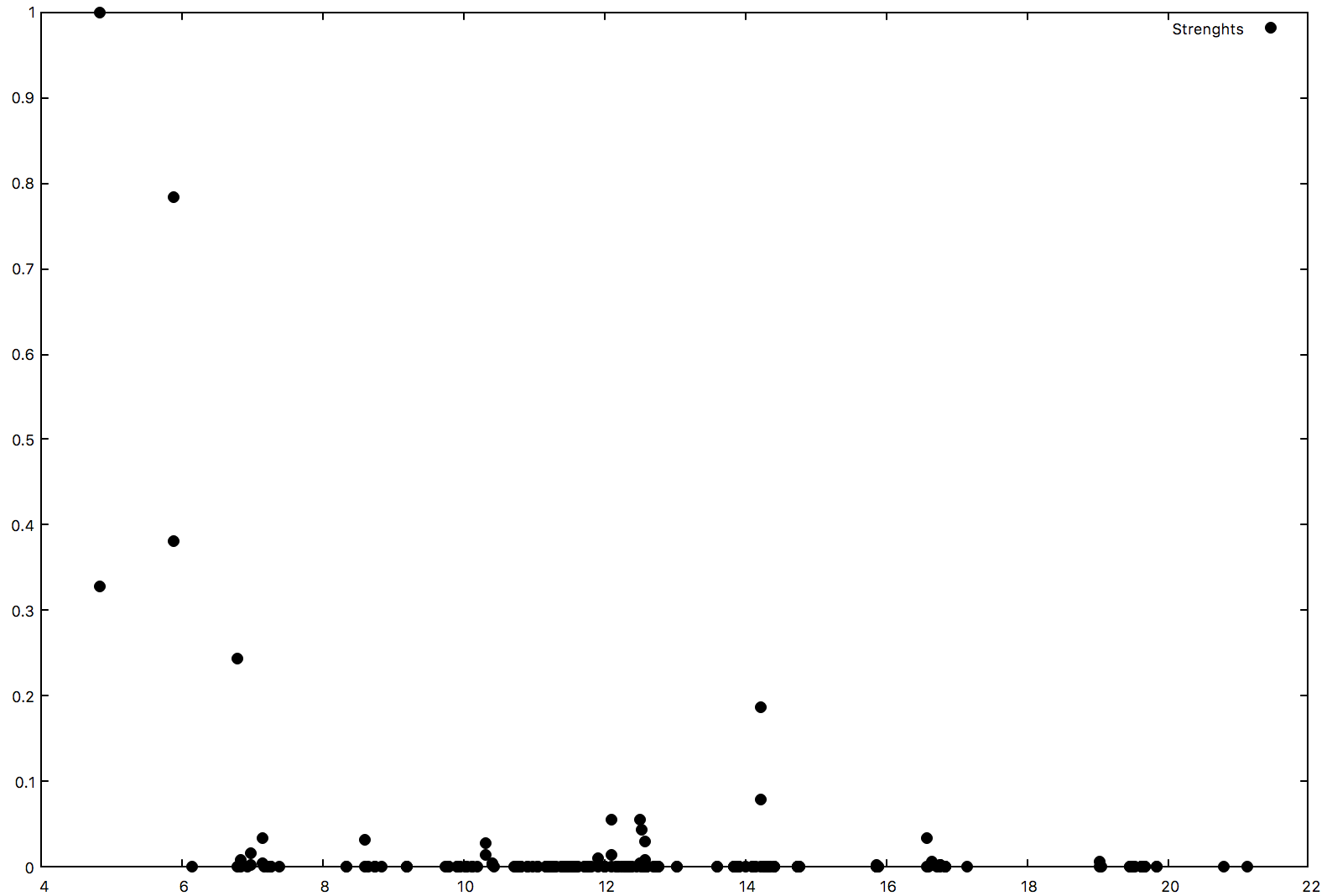
$ ypp -J 2D_WR_WC -e s 1

We are sorting the excitons for the q-index = 1 (optical limit q=0). The new generated file o-2D_WR_WC.exc_qpt1_E_sorted (o-2D_WR_WC.exc_qpt1_I_sorted ) reports the energies of the excitons and their Dipole Oscillator Strengths sorted by energy (Index).

Open the first file and look inside. The first exciton is at 4.83 eV and the second one has the highest strength (normalized to 1)

Or you can make a plot

$ gnuplot

gnuplot> set style line 2 lc rgb 'black' pt 7 # circle gnuplot> plot 'o-2D_WR_WC.exc_qpt1_E_sorted' with points ls 2 title 'Strenghts'

Attention the convergence of these results with different k-points grids is mandatory!

Calculate the exciton oscillator strenght and amplitude

We can now analyze the excitons in terms of single-particle states, to do that create the appropriate input

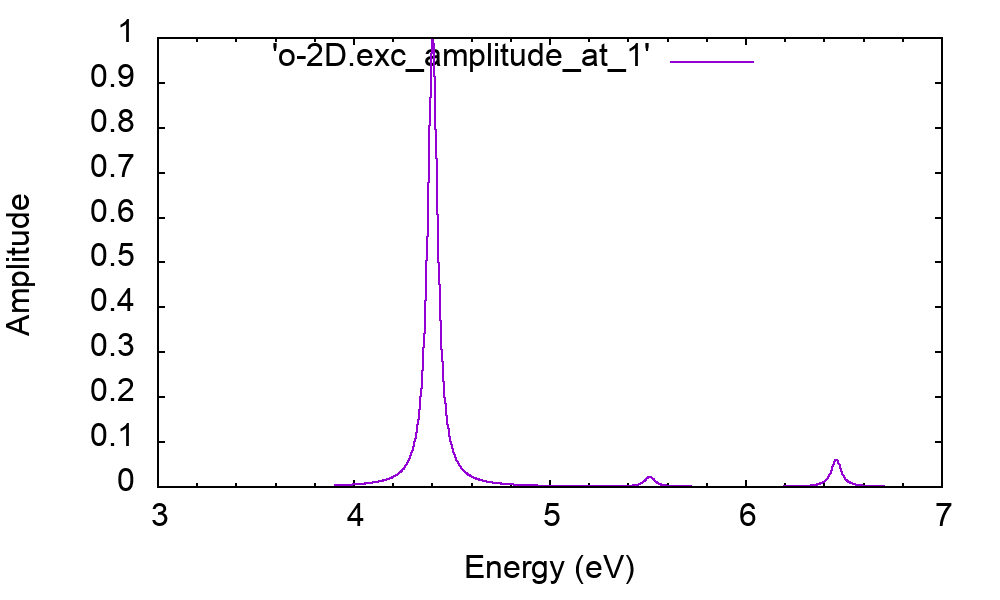
$ ypp -F ypp_AMPL.in -J 2D_WR_WC -e a 1 

Suppose you wish to analyze the first 5 excitons then change this line as:

States= "1 - 5"              # Index of the BS state(s)

Close the input and run ypp

$ ypp -F ypp_AMPL.in -J 2D_WR_WC

$ls  o*exc*at*
o-2D_WR_WC.exc_qpt1_amplitude_at_1 o-2D_WR_WC.exc_qpt1_weights_at_1 ...

For an exciton [math]\displaystyle{ |\lambda\gt }[/math] , o-2D_WR_WC.exc_qpt1_weights_at_* report the Weights

and o-2D_WR_WC.exc_qpt1_amplitude_** report the amplitudes

Open the file o-2D_WR_WC.exc_weights_at_1

#  Band_V     Band_C     K  ibz     Symm.      Weight     Energy
#
 4.000000   5.000000   7.000000   2.000000   0.922095   4.401093
 4.000000   5.000000   7.000000   1.000000   0.922086   4.401093
The first exciton is  essentially done of only single particle transitions from VBM to CBM at K (last k-point of the grid).

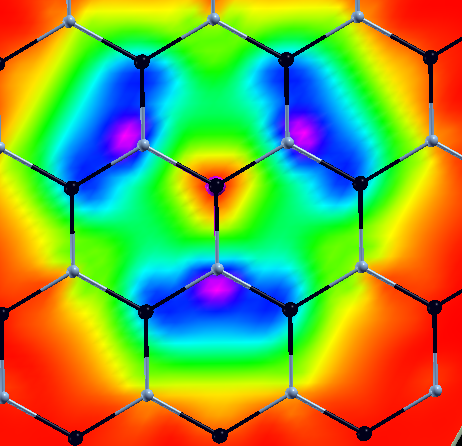
Plot the exciton spatial distribution

To see the spatial character of the exciton YPP writes the exciton spatial distribution, in other words the probability to find the electron somewhere in the space when the hole is fixed in a give position. Different output formats can be selected and 1D,2D,3D plots done. Create the input and change the size of the cell where to see the exciton. Note that If the k-grid of the BSE simulation is a NxNx1 the exciton has an induced fictitious periodicity every Nx Nx1 Cell of the simulation. For hBN-2D this is not a problem because the exciton is strongly localized but in other systems with more delocalized excitons to look at the real exciton size it is necessary to use very large k-grids in the BSE

$ ypp -F ypp_WF.in -J 2D_WR_WC  -e w  1

excitons                     # [R] Excitons
wavefunction                 # [R] Wavefunction
Format= "x"                  # Output format [(c)ube/(g)nuplot/(x)crysden]
Direction= "12"               # [rlu] [1/2/3] for 1d or [12/13/23] for 2d [123] for 3D
FFTGvecs=  3951        RL    # [FFT] Plane-waves
States= "1 - 1"              # Index of the BS state(s)
Degen_Step=   0.0100   eV    # Maximum energy separation of two degenerate states
% Cells
 5 | 5 | 1 |                             # Number of cell repetitions in each direction (odd or 1)
%
% Hole
2.4     | 1.400     | 0.00     |        # [cc] Hole position in unit cell

Close the input and run ypp

$ ypp -F ypp_WF.in -J 2D_WR_WC 

$ xcrysden --xsf o-2D_WR_WC.exc_2d_1.xsf

Plot electron/hole average density (only in Yambo 5.0)

Another way to analyze excitons, it is the possibility to plot the average electron/hole densities defined as:

to generate the corresponding input just type

ypp -F ypp_WF.in -e w -avehole

and choose the exciton you want to plot. The electron/hole average densities correspond to generalized valence/conduction orbitals for a given exciton. They are interesting in particular for molecular crystals because they allow distinguishing charge-transfer versus Frenkel excitons, from the relative position of the electron/hole densities.

Interpolate exciton dispersion (only in Yambo 5.x)

Starting from Yambo 5.x it is possible to calcaulte excitons at finite momentum q. The momentum can be specified with the variable

%BSEQptR
 iq_start | iq_end |                             # [BSK] Transferred momenta range
%

where iq_start and iq_end is the first and last index of momentum in the irreducible Brillouin zone (IBS). You can find the list of q-vectors in the r_setup report. If you calculate the BSE for all q-points in the IBZ, then you can interpolate the exciton dispersion along any direction of the full Brillouin zone(BZ) using the interpolation scheme of PRB 38 p2721, by doing ypp -s i and setting:

excitons                         # [R] Excitonic properties
interpolate                      # [R] Interpolate
States= "1 - 4"                  # Index of the BS state(s)
INTERP_mode= "BOLTZ"                # Interpolation mode (NN=nearest point, BOLTZ=boltztrap aproach)
% INTERP_Grid
 -1 |-1 |-1 |                             # Interpolation BZ Grid 
%
BANDS_steps= 30                  # Number of divisions
cooIn= "rlu"                     # Points coordinates (in) cc/rlu/iku/alat
cooOut= "rlu"                    # Points coordinates (out) cc/rlu/iku/alat
%BANDS_kpts                      # K points of the bands circuit
0 | 0 | 0 |
0.333333333333333 | 0.33333333333333 | 0 | 
%

this input file will interpolate with 30 steps the first 4 excitons energies along the line Gamma->K.