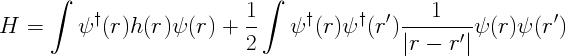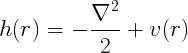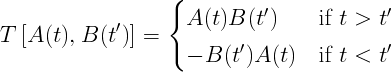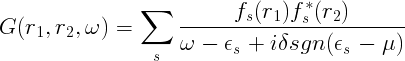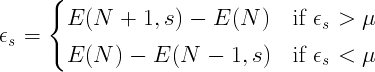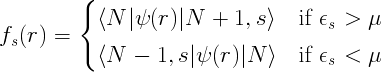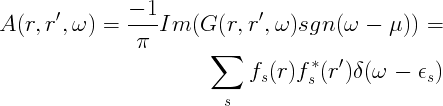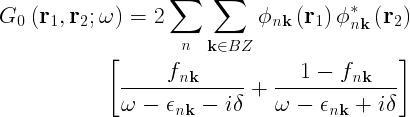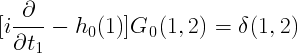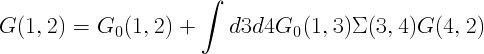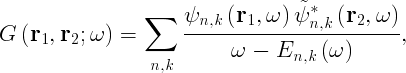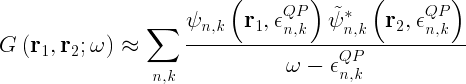Single particle Green's function: Difference between revisions
(Created page with "=== The single-particle Green's function === In this section the basic concepts about the Green's function method will be introduced. For a detailed description we refer the...") |
No edit summary |
||
| Line 3: | Line 3: | ||
In this section the basic concepts about the Green's function method will be introduced. For a detailed description we refer the reader to the many books about many-particle physics present in the literature. In the second quantized formulation the hamiltonian of N interacting electrons in an external potential v(r) can be written in term of field operators as | In this section the basic concepts about the Green's function method will be introduced. For a detailed description we refer the reader to the many books about many-particle physics present in the literature. In the second quantized formulation the hamiltonian of N interacting electrons in an external potential v(r) can be written in term of field operators as | ||
[[File: | [[File:PIC doc G-10.png|x50px|center|alt alternate text]] | ||
where | where | ||
Revision as of 12:57, 13 September 2017
The single-particle Green's function
In this section the basic concepts about the Green's function method will be introduced. For a detailed description we refer the reader to the many books about many-particle physics present in the literature. In the second quantized formulation the hamiltonian of N interacting electrons in an external potential v(r) can be written in term of field operators as
where
In this context the single-particle Green's function is formally defined as
where |N> is the ground state vector of the N-particles interacting system, and where
are creation and annihilation field operators written in the Heisenberg picture. And the time ordered product between to operators A and B is defined as:
From the definition of time-ordered product it comes out that the Green's function describes the propagation of an electron for positive time, viceversa for negative time it describes the propagation of an hole. From the knowledge of the Green's function it is possible to obtain many properties of the many-body system, such as : the ground state total energy of the system, the expectation value of any single-particle observable in the ground state, the excitation spectra. Inserting the set of eigenstates |N+1,s> and |N-1,s> of the (N+1) particles (and (N-1) particles) hamiltonian it is possible to obtain the so-called Lehmann representation of the Green's function:
where
and
The poles of the Green's function are thus seen to correspond to the electron addition or removal energies. While for finite systems the poles are discrete quantities, when approaching the thermodinamic limit the discrete poles merge in a continuum and we have to analitically continue the Green's function to the complex plane before taking the limit. Let us now define another quantity which plays an important role in the quasi-particle spectra and is directly connected to the experiments, which is the spectral function. It is a quantity proportional to the imaginary part of the Green's function and has the meaning of density of states per unit energy:
The non-interacting representation
When the Hamiltonian contains only single-particle potentials, like in any mean-field theory (like Hartree, Hartree-Fock, Kohn-Sham ...) the single-particle Green's function is
and where the following equation is satisfied:
Where the h_0 is the single particle hamiltonian and the compact notation (i,j) stands for two pairs of space, time and spin coordinates,
The Dyson equation and the Quasi-particle concept
The Lehman representation sheds light on the physical information contained in the Green's function but actually it does not provide any insight on how to get it. It can be shown that the Green's function of the interacting system can be obtained solving an integral equation, the so-called Dyson equation, when the Green's function of the non interacting system and the self-energy (which is a non local, non hermitian and energy dependent operator) are known:
Moreover it can be shown that the temporal Fourier transformed Green's function, solution of the Dyson equation, admits a biorthormal representation,
where
are the left and right eigenvectors of the Hamiltonian
Since the self-energy operator is not hermitian the eigenvectors are not necessary orthonormal and the eigenvalues are not necessary real. The quasi-particle concept comes from the assumption that it is possible to describe the main energy dependence of the Green's function with a sum of well defined isolated complex poles
with the quasi-particle energies defined by
An intuitive way to understand what is a quasi-particle is to think that when a bare particle, like an electron or an hole, enters an interacting system, it perturbs the particles in its vicinity and is dressed by a polarization cloud of the sorrouding particles, becoming a so-called quasi-particle and, in many cases, it is possible to describe the strongly interacting electrons by the usage of these quasi-particles which are weakly interacting. In principle the quasi-particle paradigm is known to be meaningful only for excitations in a small range of energy near the Fermi level, but it has become a common habit to call quasi-particles also excitations far away from the Fermi level. In general if a quasi-particle has to be regardered as a quasi-particle or not is recognized by photoemission and inverse photoemission experiments. If a sharp peak appears in the spectrum then one is authorized to adopt the Fermi liquid paradigm and speak of a quasi-aprticle.
References
- L. Fetter and J.D. Walecka Quantum theory of Many-Body Systems, McGraw-Hill, New York, N.Y. 1981.