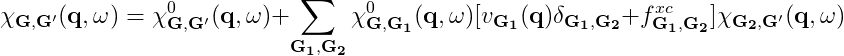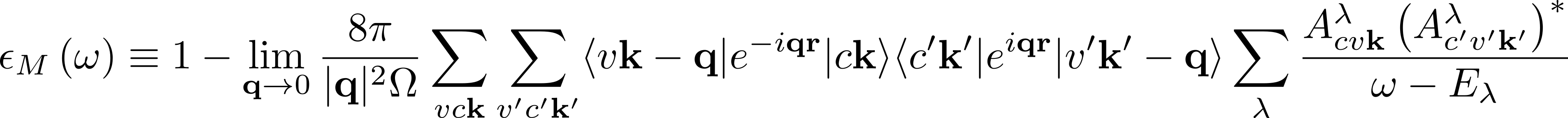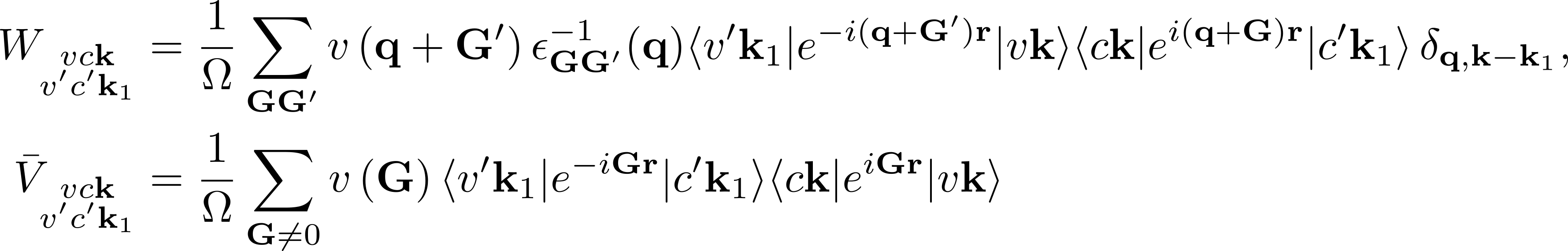How to choose the input parameters

In the previous tutorial, you have been guided step-by-step through the calculations of the optical spectrum of bulk hBN by solving the Bethe-Salpeter equation. The values for the relevant input parameters have then been given to you.

In this tutorial you will learn how to choose those parameters. These parameters are related either to the truncation of infinite sums or to the approximations of infinitesimal with small, but finite quantities. A wrong choice of these parameters can lead to inaccurate or even physically wrong results. One then needs to run a series of calculations by changing the parameters till the results are converged , meaning they are changing by a negligible amount. This is a tedious still essential part of the calculations.

Note that all the following operations can be automated. A useful python-based interface to yambo, yambopy, can be used for this purpose. It is worth however to go at least once through the pain of a 'by-hand' convergence study so to better understand the automated process.

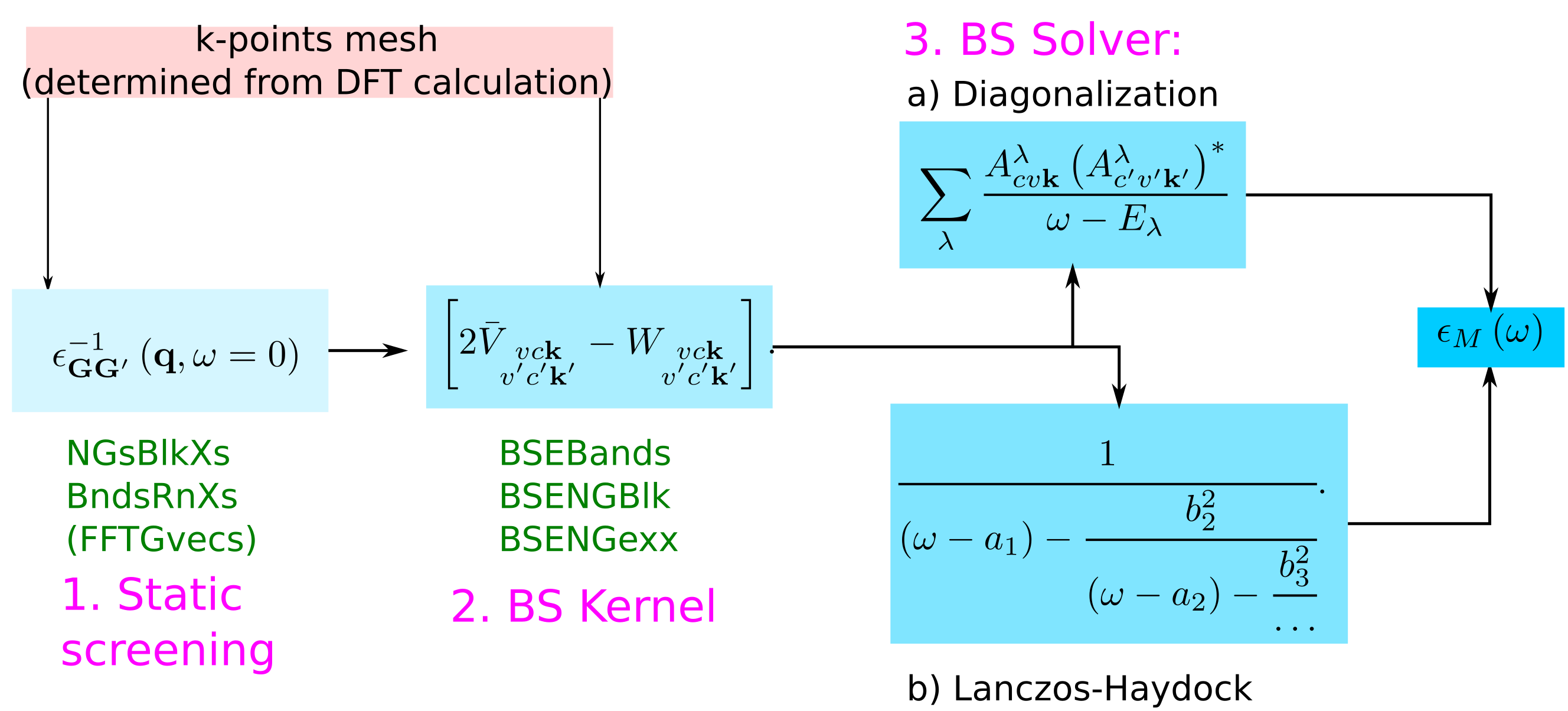
Coming back to the scheme to calculate the macroscopic dielectric matrix within Bethe-Salpeter (BS), here the list of the parameters that have to be determined by convergence studies:

First the parameters for the screening have to be determined, then the parameters for the BS kernel. Finally the convergence with respect to the choice of the k-mesh needs to performed.

Before starting

You need to

• download COMPLETE
• Have completed the following tutorials:

- First steps: a walk through from DFT to optical properties - Calculating optical spectra including excitonic effects: a step-by-step guide (or be familiar with their content)

Convergence of the static screening

The parameters that need to be converged can be understood by looking at the equations:

where χ_GG' is given by

• NGsBlkXs : The dimension of the microscopic inverse matrix, related to Local fields
• BndsRnXs : The sum on bands in the independent particle χ⁰_GG'

Furthermore as shown in this tutorial one can reduce the value of

• FFTGvecs

since generally, fewer G-vectors are needed than what are needed in DFT calculations. This can be critical for large calculations, or for supercells with a lot of vacuum. Note that this parameter appear only when the input is generated specifying the verbosity level -V RL

The convergence for the static screening then is similar to the convergence of other response functions and the plasmon pole in GW calculations and won't be covered here. Note in fact that you can re-use the database obtained (and converged) from a previous plasmon pole calculation as long as the same k-points are used.

Convergence of the macroscopic dielectric function

In the expression for the macroscopic dielectric function

depends on the summation over the pair of quasiparticle states vck.

• BSEBands : defines the vc pairs.
• the k-point mesh of the DFT calculations defines the k

Basically we need a large enough basis of transitions (pair of quasiparticle states) to correctly describe the excitons in the energy region of interest.

Furthermore, in the kernel part

summations over G vectors appear:

• BSENGblk: defines the screened interaction block size (double sum in W).
• BSENGexx: defines the components of Hartree potential (the sum in V).

In the following we will see how the spectrum depends on these parameters.

Prepare the common databases

Enter the 6x6x2 directory and run the initialization. For all the calculations in this sessions you can fix the screening parameters, and thus calculate the screening once for all. Following the scheme we learned in previous tutorial:

- Create the input for calculating the screening:

$ yambo -F 02_screening.in -b

- Modify the input as follows

NGsBlkXs = 4 Ry
%BndsRnXs
 1 | 40 |
%
%LongDrXS
 1.000 | 1.000 | 1.000|
%

- Run the calculation for the screening

$ yambo -F 02_screening.in 

As we do not specify a particular prefix, the screening databases ndb.dip_iR_and_P, ndb.em1s are saved in the SAVE folder and visible to all the subsequent jobs you will launch is this directory.

Convergence with the cut-off for reciprocal lattice vectors sums

Create the input for calculating the macroscopic dielectric function:

$ yambo -F 03_bse.in -o b -k sex -y d -V qp

Which combines the BS kernel + BS solver (diagonalization) runlevels - Modify the input as follows

BSENGexx = 30 Ry
BSENGBlk = 4 Ry
% BSEBands
 6 | 10 |       
%
% BEnRange
  2.00000 | 8.00000 | eV    
%
BEnSteps= 100      
% BDmRange
  0.10000 |  0.10000 | eV    
%
% BLongDir
 1.000000 | 1.000000 | 0.000000 | 
%
% KfnQP_E 
 1.440000 | 1.000000 | 1.000000 |
%
BSHayTrs= 0.02000

Launch the calculation:

$ yambo -F 03_bse.in -J 3D_4Ry_GBlk

This produces the file with the optical spectrum o-3D_4Ry_GBlk.eps_q1_diago_bse.

Open the 03_bse.in in an editor and changes:

BSENGBlk = 3 Ry

while leaving the rest untouched. Launch the calculation:

$ yambo -F 03_bse.in -J 3D_3Ry_GBlk

This produces the file with the optical spectrum o-3D_3Ry_GBlk.eps_q1_diago_bse. BSENGBlk= 2 Ry Repeat this operation for BSENGBlk= 2 Ry and BSENGBlk= 1 Ry. Remember to change the prefix correspondingly so that you can later on identify the job, e.g. -J 3D_3Ry_GBlk for BSENGBlk= 2 Ry. etc.

Finally plot the obtained optical spectra:

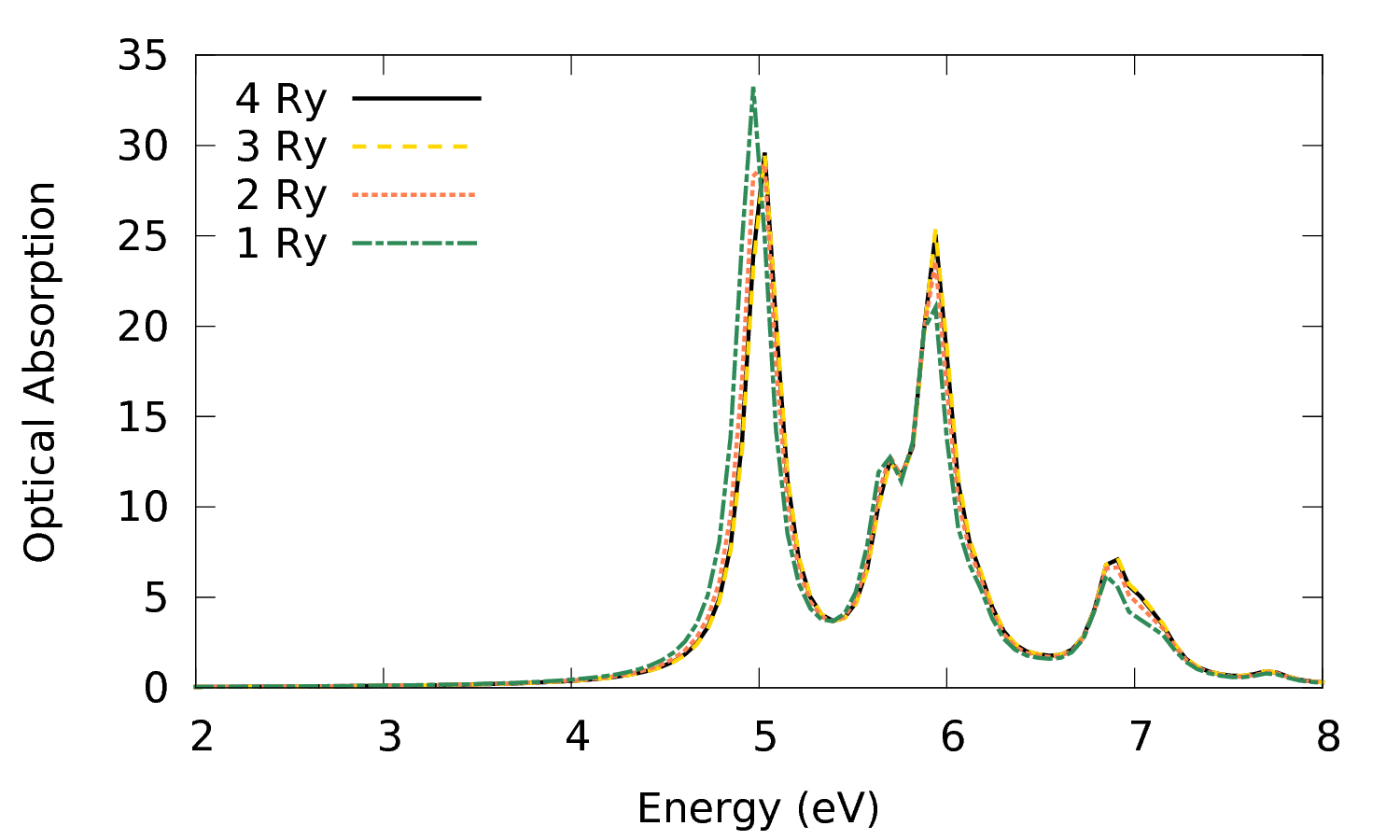
$ gnuplot
plot  'o-3D_4Ry_GBlk.eps_q1_diago_bse' w l t '4 Ry','o-3D_3Ry_GBlk.eps_q1_diago_bse' w l t '3 Ry',  'o-3D_2Ry_GBlk.eps_q1_diago_bse' w l t '2 Ry', 'o-3D_1Ry_GBlk.eps_q1_diago_bse' w l t '1 Ry'

This shows that BSENGBlk= 2 Ry gives already a results close to convergence and we can confidently lower BSENGBlk to 2,3 Ry.

Repeat now the same procedure with BSENGexx. Change the value to 10 Ry and 20 Ry. Remember to change the prefix correspondingly so that you can later on identify the job, e.g. -J 3D_10Ry_Gexx for BSENGexx= 10 Ry. etc.

Finally plot the obtained optical spectra:

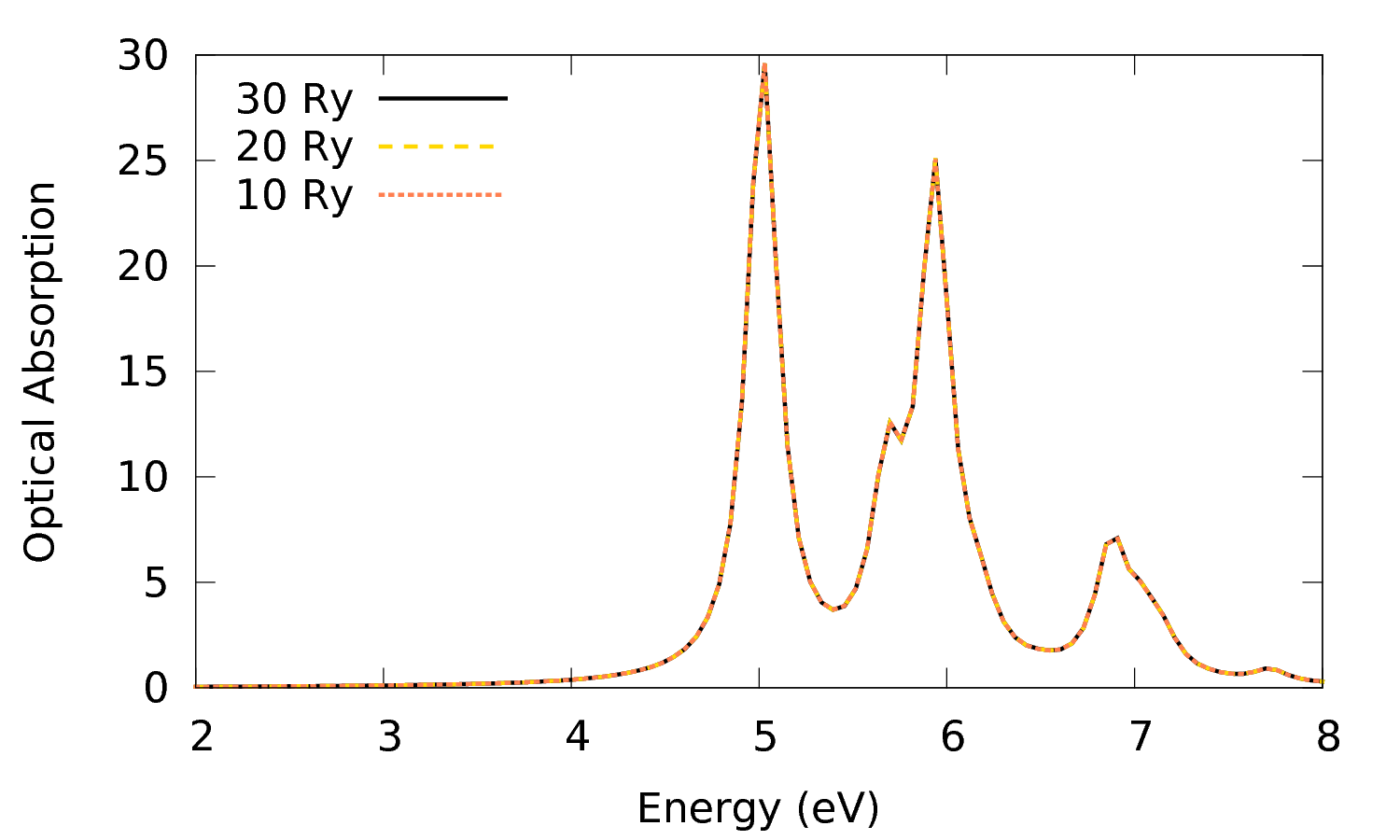
$ gnuplot
 plot  'o-3D_4Ry_GBlk.eps_q1_diago_bse' w l t '30 Ry' ls 1,'o-3D_20Ry_Gexx.eps_q1_diago_bse' w l t '20 Ry',  'o-3D_10Ry_Gexx.eps_q1_diago_bse' w l t '10 Ry'

The plot shows that already with BSENGexx= 10 Ry the spectrum is converged and the cut-off can be lowered to this value.

Convergence with the BS bands

You can then repeat the procedure above keeping fixed all parameters except

% BSEBands
6 | 10 |       
%

Typically only the bands close to the Fermi energies contributes to the spectrum. If the energy separation between two bands is much larger than the spectral energy range, you can assume the corresponding transitions are not contributing to the spectra. Repeat then the calculation for the optical spectrum using the following band ranges: 7-10, 8-10, 6-9, 7-9 and 8-9. When launching the job remember to identify your job with a recognizable name, e.g. -J 3D_7-9_BND.

Plot then the optical spectra obtained from the different runs:

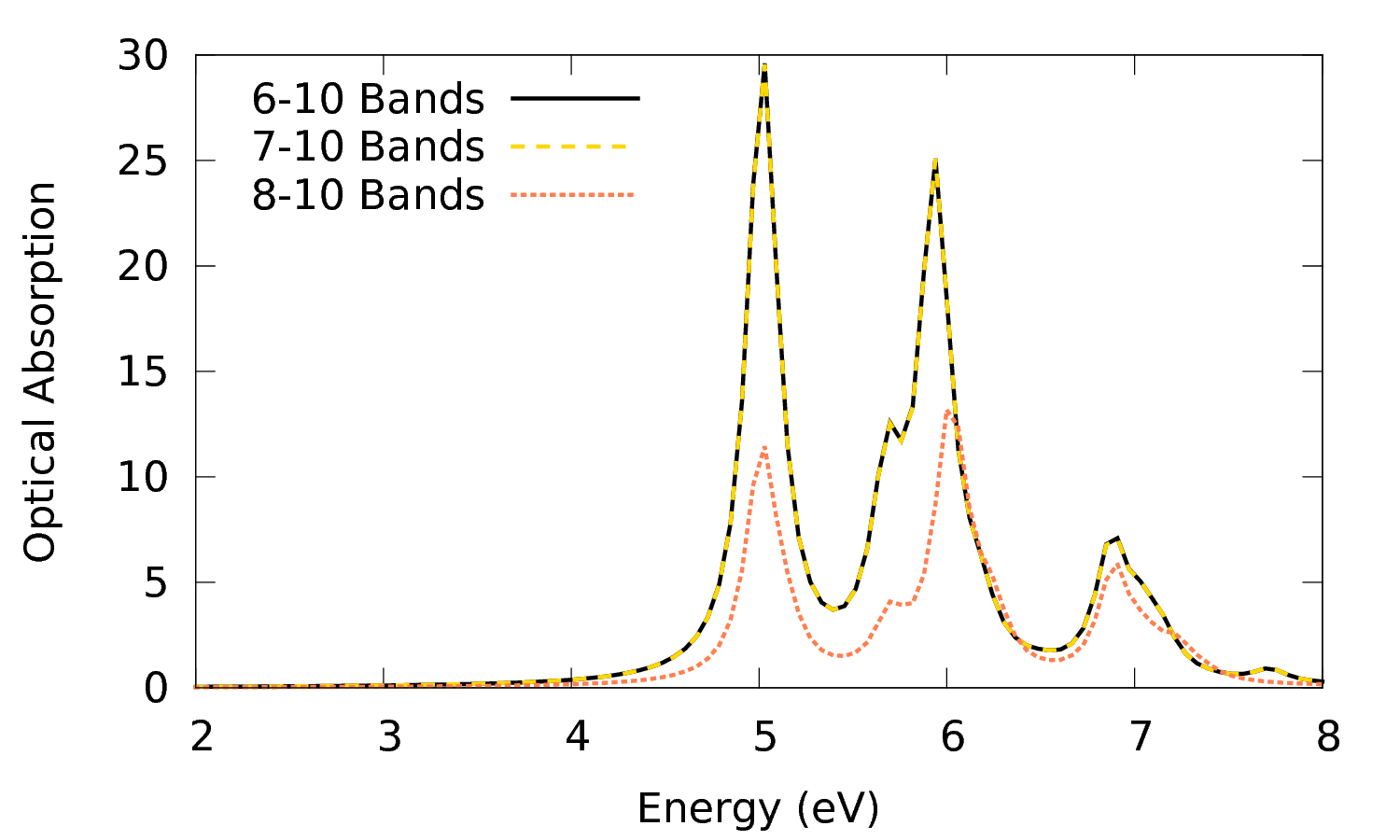
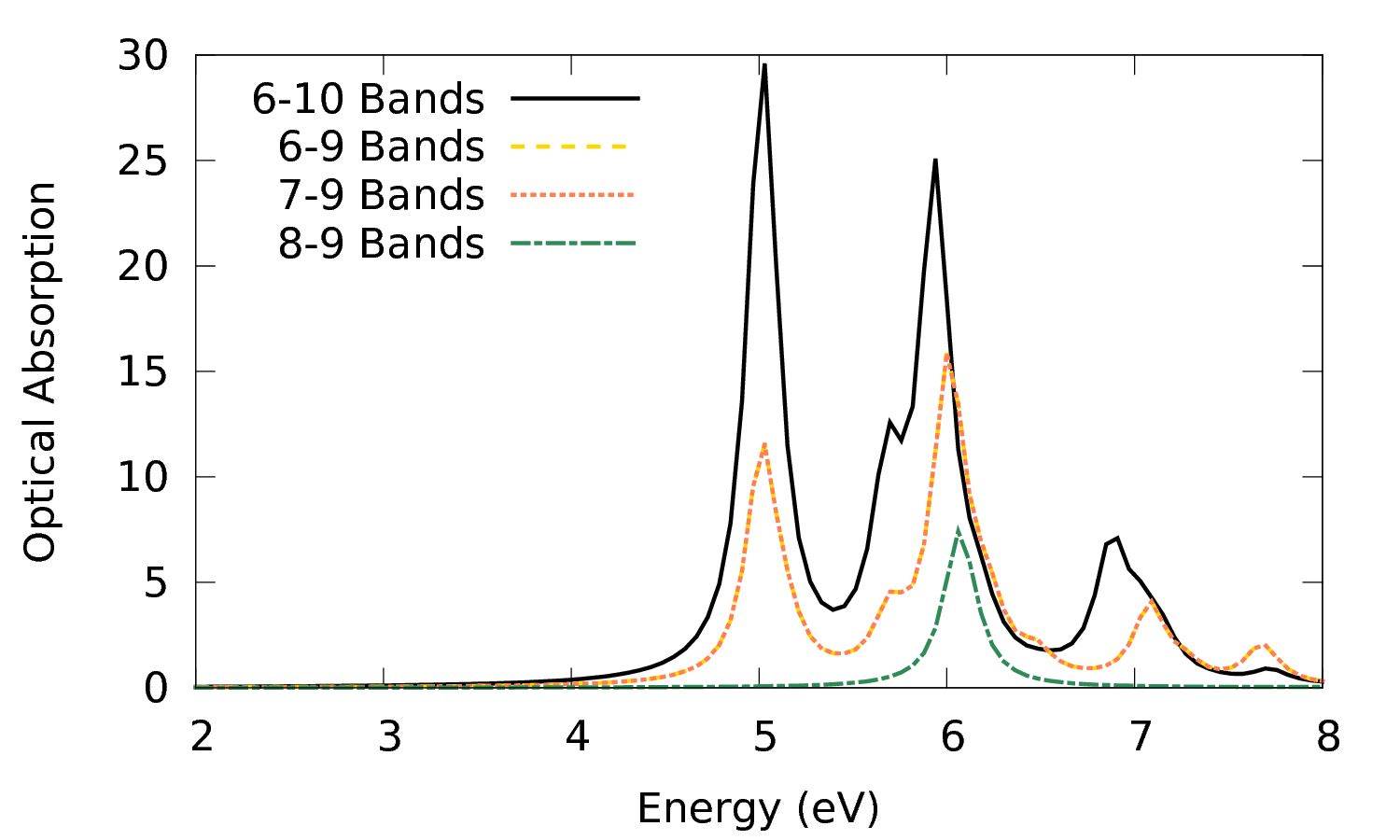
$ gnuplot
plot  'o-3D_4Ry_GBlk.eps_q1_diago_bse' w l t '6-10 Bands','o-3D_7-10_BND.eps_q1_diago_bse' w l t '7-10 Bands', 'o-3D_8-10_BND.eps_q1_diago_bse' w l t '8-10 Bands'
plot  'o-3D_4Ry_GBlk.eps_q1_diago_bse' w l t '6-10 Bands','o-3D_6-9_BND.eps_q1_diago_bse' w l t '6-9 Bands', 'o-3D_7-9_BND.eps_q1_diago_bse' w l t '7-9 Bands', 'o-3D_8-9_BND.eps_q1_diago_bse' w l t '8-9 Bands'

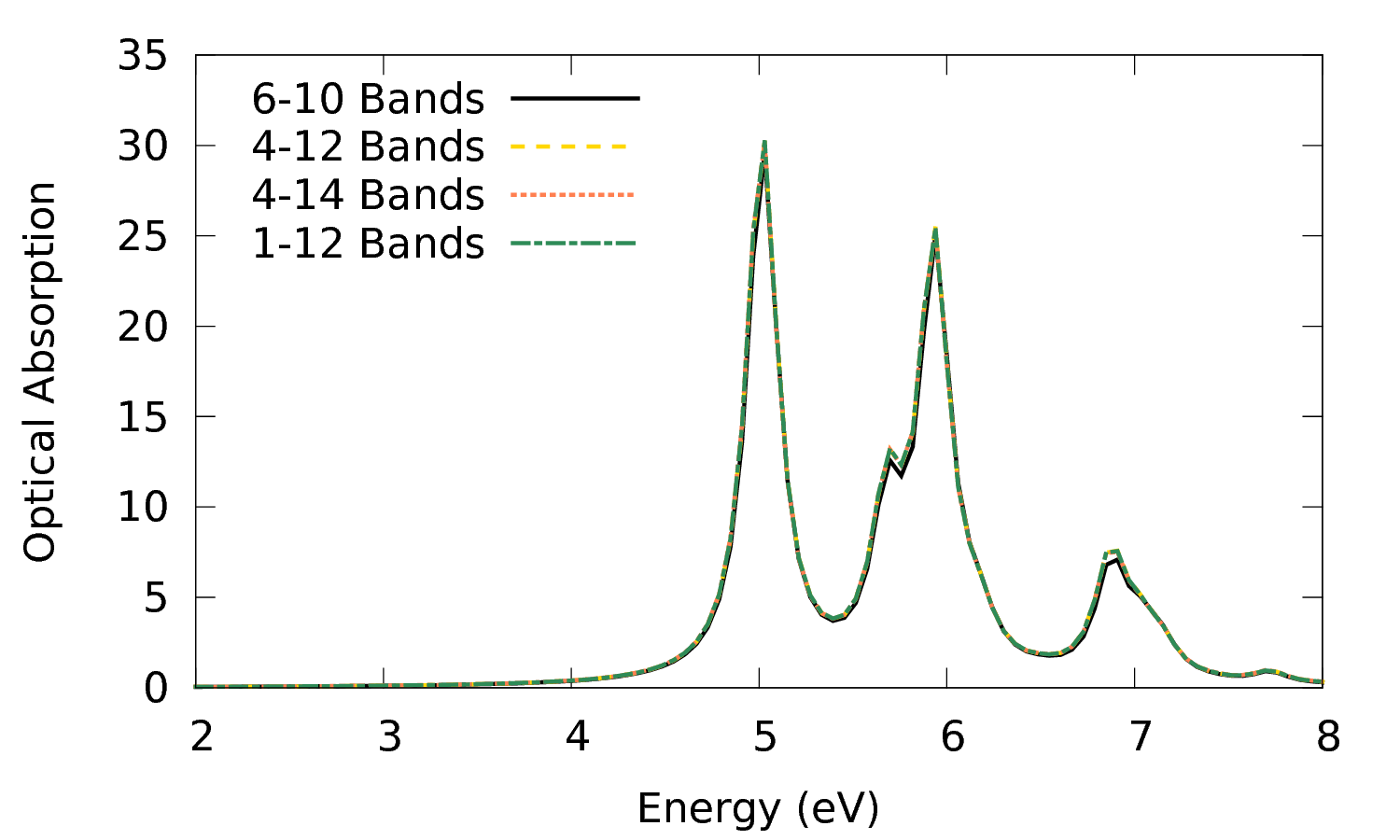
From the plots we see we need to include valence bands from at least 6-7 (those bands are degenerate at several high symmetry points of the Brillouin zone) and band 10. To see if this is sufficient you can try to include more bands. For example you can prepare and run calculations with the following bands ranges: 1-12, 4-12, 4-14 and plot the results

$ gnuplot
plot  'o-3D_4Ry_GBlk.eps_q1_diago_bse' w l t '6-10 Bands','o-3D_4-12_BND.eps_q1_diago_bse' w l t '4-12 Bands', 'o-3D_4-14_BND.eps_q1_diago_bse' w l t '4-14 Bands', 'o-3D_1-12_BND.eps_q1_diago_bse' w l t '1-12 Bands' ls 4

Which is showing that the spectrum changes only marginally when adding those bands.

Convergence with the k-point mesh

After you converged the parameters for the screening, the bands range and the cut-offs on the summations over reciprocal lattice vectors in the kernel, you need to study the dependence on the k mesh. This parameter cannot be changed in yambo. For each k mesh you need to run a separate non-self consistent DFT calculation (on top of a converged self-consistent one) and then generate the corresponding SAVE folders. Be careful to change only the k mesh.

For this exercise the SAVE databases for different meshes were generated beforehand and are contained in the corresponding folders:

9x9x3 12x12x4 15x15x5 18x18x6

Following the scheme we learned in previous tutorial:

- Enter the 9x9x3 directory - Run the initialization - Create the input for calculating the screening:

 $ yambo -F 02_screening.in -J 3D_993 -b

- Modify the input as follows

NGsBlkXs = 4 Ry
%BndsRnXs
1 | 40 |
%
%LongDrXS
1.000 | 1.000 | 1.000|
%

- Run the calculation for the screening

$ yambo -F 02_screening.in -J 3D_993

- Create the input for calculating the macroscopic dielectric function:

$ yambo -F 03_bse.in -J 3D_993 -o b -k sex -y h -V qp

Which combines the BS kernel + BS solver (Lanczos-Haydock) runlevels - Modify the input as follows

BSENGexx = 30 Ry
BSENGBlk = 4 Ry
% BSEBands
 6 | 10 |       
%
% BEnRange
  2.00000 | 8.00000 | eV    
%
BEnSteps= 200      
% BDmRange
  0.10000 |  0.10000 | eV    
%
% BLongDir
 1.000000 | 1.000000 | 0.000000 | 
%
% KfnQP_E 
 1.440000 | 1.000000 | 1.000000 |
%
BSHayTrs= 0.02000

- Launch the calculation:

$ yambo -F 03_bse.in -J 3D_993

-Repeat the procedure for the 12x12x4 (it will take few minutes) with the difference you will use a different prefix: -J 3D_12124.

The convergence on the k-point is certainly the most tedious and expensive part. Note that for the two larger meshes the calculations of both the screening and kernel take about 10 to 30 minutes each. If short of time/resources postpone these calculations. If you have the time and computational resources repeat the above procedure for 15x15x5 and 18x18x6. Note that the BS kernel database is very (too!) large and you need to fragment it to speed up the IO. To do that after you generated and modified the input invoke yambo again as:

$ yambo -F 03_bse.in -J 3D_15155 -o b -k sex -y h -V io

and modify the variable

 DBsFRAGpm= "+BS"

Then launch the calculation

$ yambo -F 03_bse.in -J 3D_15155

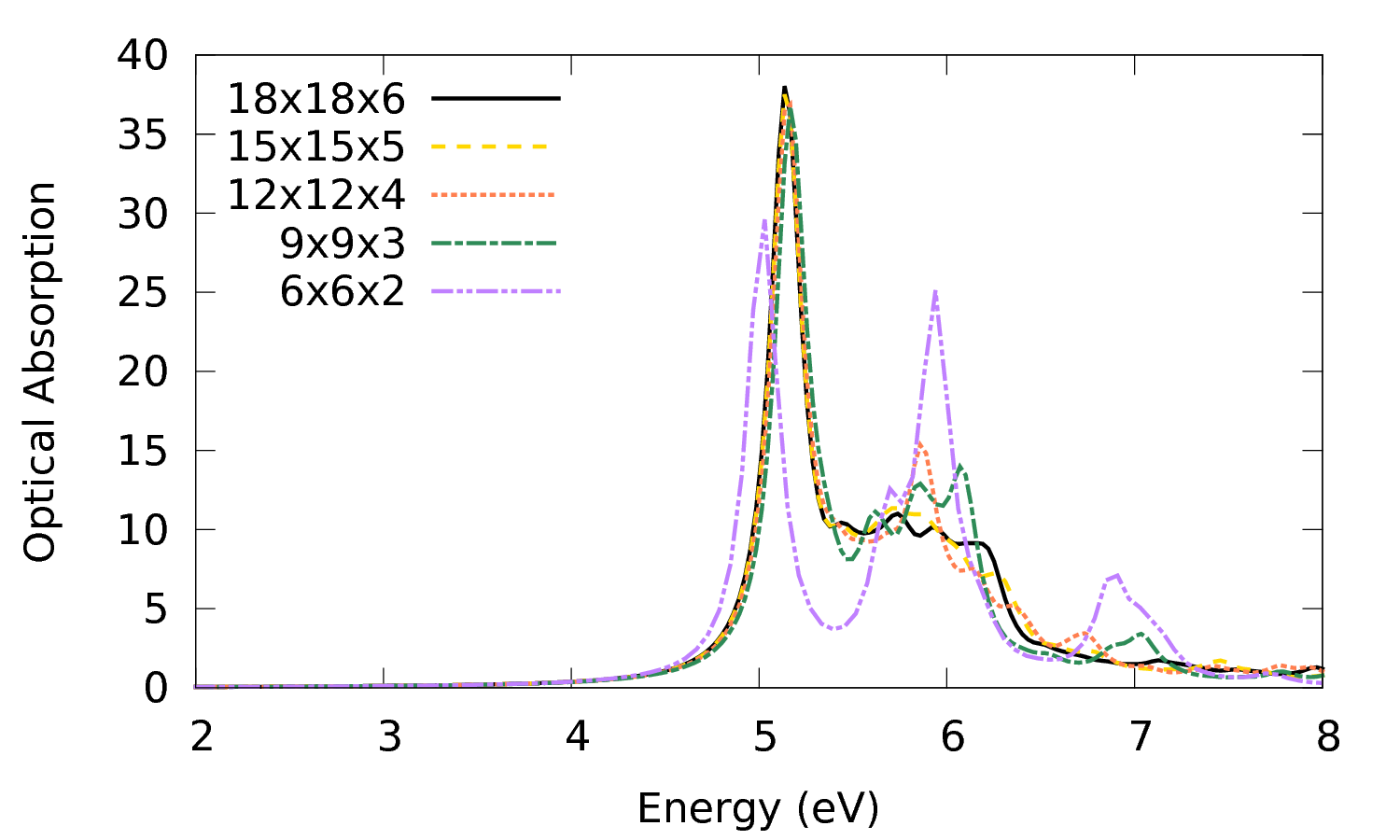
If you correctly followed the above procedure you have a file of the optical absorption spectrum for each mesh, e.g. o-3D_993.eps_q1_haydock_bse. To see at the effect of k-points plot those files with gnuplot:

$ gnuplot
> plot '18x18x6/o-3D_18186.eps_q1_haydock_bse' w l t '18x18x6, '15x15x5/o-3D_15155.eps_q1_haydock_bse' w l t '15x15x5', . . .
  . . . '12x12x4/o-3D_12124.eps_q1_haydock_bse' w l t '12x12x4, '9x9x3/o-3D_993.eps_q1_haydock_bse' w l t '9x9x3', '6x6x2/o-3D_662.eps_q1_haydock_bse' w l t '6x6x2'

From this plot you can notice that:

• results with the 6x6x2 mesh are clearly non converged: the first peak is too red shifted, the peak at 6 eV too sharp and intense and there is an 'extra' peak at 7 eV
• both the position and shape of the first peak are practically converged with the 9x9x3 mesh
• conversely the second peak is still not fully converged with the 18x18x6

The difference behavior in the convergence of the two features depends on the localization of the exciton. The sharp first peak suggests a quite localized exciton. The shape of the second peak a much more delocalized exciton. A finer k mesh, corresponds in direct space, to considering a larger amount of unit cells. Then when the excitation is delocalized over a large number of unit cells a very fine k mesh is needed. Typically a too coarse k mesh induces an artificial localization of the excitons which then correspond to artefacts in the spectrum (similar to what is observed for the 6x6x9). A nice, instructive discussion on wrong deductions from unconverged k mesh calculations can be found in the Appendix of Molina-Sanchez et al. (2013).

Summary

To sum-up the results from this tutorial you have found that for the system under study:

• BSENGBlk= 3 Ry
• BSENGexx= 10 Ry
• BSEBands from 6 to 10
• To converge the position and shape of the first exciton peak a 12x12x4 mesh is sufficient. For the second exciton peak a mesh larger than 18x18x6 would be needed (indeed Wirtz and co-workers found a k-mesh 24x24x10 was needed.)