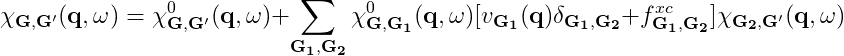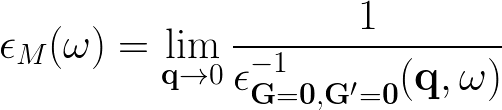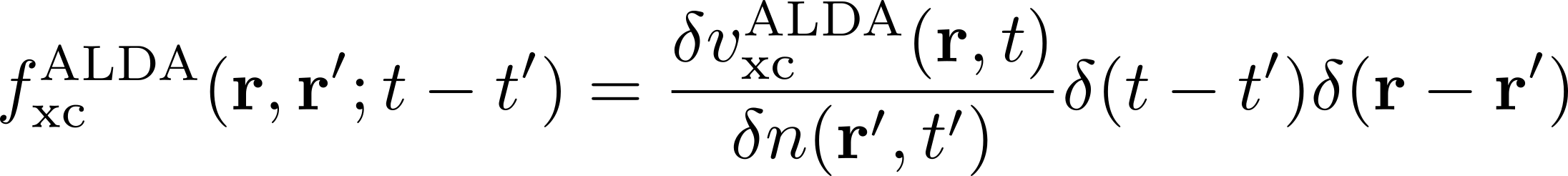Time-dependent density functional theory (standard kernel): Difference between revisions
No edit summary |
|||
| Line 64: | Line 64: | ||
* The ALDA kernel, and expanded G-vectors in the screening and in the xc kernel up to 3 Ry (about 85 G-vectors) | * The ALDA kernel, and expanded G-vectors in the screening and in the xc kernel up to 3 Ry (about 85 G-vectors) | ||
==Optics runlevel== | ==Optics runlevel: ALDA== | ||
Save the input file and launch the code, keeping the command line options as before (i.e., just remove the lower case options): | Save the input file and launch the code, keeping the command line options as before (i.e., just remove the lower case options): | ||
$ yambo -F yambo.in_ALDA -J 3D_ALDA | $ yambo -F yambo.in_ALDA -J 3D_ALDA | ||
| Line 90: | Line 90: | ||
Yambo tutorial image | Yambo tutorial image | ||
==Summary== | ==Summary== | ||
Revision as of 16:15, 16 April 2017
In this tutorial you will learn how to calculate optical spectra at the time-dependent density-functional theory level for bulk hBN.
Background
The macroscopic dielectric function is obtained by including the so-called local field effects (LFE) in the calculation of the response function. Within the time-dependent DFT formalism this is achieved by solving the Dyson equation for the susceptibility X. In reciprocal space this is given by:
The microscopic dielectric function is related to X by:
and the macroscopic dielectric function is obtained by taking the (0,0) component of the inverse microscopic one:
Experimental observables like the optical absorption and the electron energy loss can be obtained from the macroscopic dielectric function:
The f xc term is called the exchange-correlation (xc) kernel and describes the response of the xc potential at a time t to changes in the density at all previous times. Approximations for the xc kernel can be derived by taking the functional derivative of common approximations for the xc potential with respect to the density with the additional approximation that only instantaneous changes to the density are considered (adiabatic approximation).
Within this family we consider here the adiabatic local density approximation (ALDA)
As this module will show for bulk hBN this approximation provides spectra similar to the RPA when applied to extended systems (it has instead a significant impact on molecular excitations). One of the main problems that has been pinpointed in the literature is that ALDA and its likes miss a long range contribution essential to reproduce excitations in solids. Several approximations have been proposed to introduce this essential long range contribution.[1][2][3][4][5]
Within this family we consider here the long-range correction approximation (LRC):
where α is an empirical parameter related to the system screening.[6]
Note that approximations of this form cannot be rigorously justified within the sole time-dependent density-functional framework. Additional key quantities such as the electron density current or the macroscopic polarization (together with the corresponding xc fields) need to be considered.[7][8][9]
Prerequisites
- You must first complete the "How to use Yambo" and the "Optics at the independent particle level" and "local fields" modules
You will need:
- The
SAVEdatabases for bulk hBN - The
yamboexecutable gnuplot, for plotting spectra
Choosing input parameters: ALDA kernel
Enter the folder for bulk hBN that contains the SAVE directory, and generate the input file. From yambo -H you should understand that the correct option is yambo -o c -k <opt> .
Where <opt> can be 'hartree' as in the tutorial on the local fields, or 'alda' or 'lrc' respectively for the ALDA and LRC approximations for the xc kernel outlined above.
Let's start by running the calculation with the ALDA kernel:
$ cd YAMBO_TUTORIALS/hBN-3D/YAMBO $ yambo (Initialization) $ yambo -F yambo.in_ALDA -V RL -J 3D_ALDA -o c -k alda
We thus use a new input file yambo.in_ALDA, switch on the FFTGvecs variable, and label all outputs/databases with a 3D_ALDA tag. Make sure to set/modify all of the following variables to:
FFTGvecs= 30 Ry # [FFT] Plane-waves Chimod= "ALDA" # [X] IP/Hartree/ALDA/LRC/BSfxc FxcGRLc= 3 Ry # [Xd] Response block size NGsBlkXd= 3 Ry # [Xd] Response block size % QpntsRXd 1 | 1 | # [Xd] Transferred momenta % % EnRngeXd 0.00000 | 20.00000 | eV # [Xd] Energy range % % DmRngeXd 0.200000 | 0.200000 | eV # [Xd] Damping range % ETStpsXd= 2001 # [Xd] Total Energy steps % LongDrXd 1.000000 | 1.000000 | 0.000000 | # [Xd] [cc] Electric Field %
In this input file, we have selected:
- the long-wavelength limit q = 0 (optical limit)
- A q parallel to the BN planes
- The ALDA kernel, and expanded G-vectors in the screening and in the xc kernel up to 3 Ry (about 85 G-vectors)
Optics runlevel: ALDA
Save the input file and launch the code, keeping the command line options as before (i.e., just remove the lower case options):
$ yambo -F yambo.in_ALDA -J 3D_ALDA ... <01s> [05] Optics <01s> [LA] SERIAL linear algebra <01s> [WF] Performing Wave-Functions I/O from ./SAVE <01s> [FFT-Rho] Mesh size: 9 9 21 <01s> [xc] Functional Slater exchange(X)+Perdew & Zunger(C) <01s> [xc] LIBXC used to calculate xc functional ...
Note that, with respect to the Hartree kernel (RPA calculations) the libxc is called to calculate the xc kernel within the ALDA, in particular the Perdew-Zunger parametrization for the correlation part of the LDA is used.
let's compare the absorption with and without the local fields included. By inspecting the o-q100.eps_q1_inv_rpa_dyson file we find that this information is given in the 2nd and 4th columns, respectively:
$ head -n30 o-3D_ALDA.eps_q1_inv_alda_dyson
- Absorption @ Q(1) [q->0 direction] : 0.7071068 0.7071068 0.0000000
- E/ev[1] EPS-Im[2] EPS-Re[3] EPSo-Im[4] EPSo-Re[5]
Plot the result:
$ gnuplot gnuplot> plot "o-3D_ALDA.eps_q1_inv_alda_dyson" u 1:2 w l t 'ALDA',"o-3D_ALDA.eps_q1_inv_alda_dyson" u 1:4 w l t 'IPA'
Yambo tutorial image
Summary
From this tutorial you've learned:
- How to compute a simple optical spectrum
- How to reduce the computational load through reducing the G-vector/energy cut off and removing the Vnl term
- How to plot different components of the dielectric tensor
- How to use the
-Joption to neatly label and organise files and databases
Links
- Next module: Local fields
- Back to First steps with yambo tutorial
- Back to tutorials menu
References
- ↑ L. Reining, V. Olevano, A. Rubio, and G. Onida, Phys. Rev. Lett. 88, 066404 (2002)
- ↑ P. E. Trevisanutto, A. Terentjevs, L. A. Constantin, V. Olevano, and F. Della Sala, Physical Review B 87, 205143 (2013)
- ↑ J. A. Berger, Phys. Rev. Lett. 115, 137402 (2015)
- ↑ S. Rigamonti, S. Botti, V. Veniard, C. Draxl, L. Reining, and F. Sottile, Phys. Rev. Lett. 114, 146402 (2015)
- ↑ S. Sharma, J. K. Dewhurst, A. Sanna, and E. K. U. Gross, Phys. Rev. Lett. 107, 186401 (2011)
- ↑ S. Botti, F. Sottile, N. Vast, V. Olevano, L. Reining, H.-C.Weissker, A. Rubio, G. Onida, R. Del Sole, and R. Godby, Physical Review B 69, 155112 (2004)
- ↑ M. Gr¨ning, D. Sangalli, C. Attaccalite, C. Physical Review B 94, 035149 (2016)
- ↑ P. L. de Boeij, F. Kootstra, J. A. Berger, R. van Leeuwen, and J. G. Snijders, The Journal of Chemical Physics 115, 1995 (2001)
- ↑ J. A. Berger, Phys. Rev. Lett. 115, 137402 (2015)