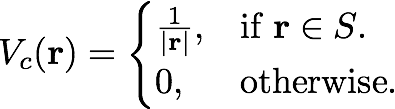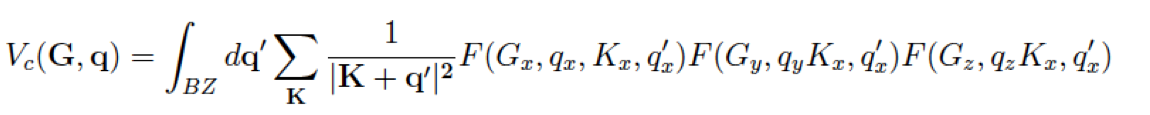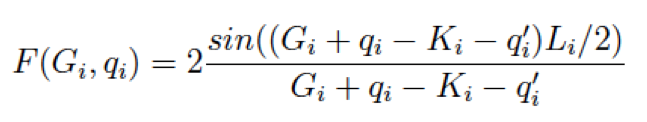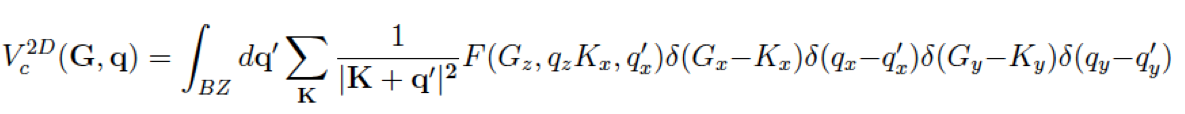How to treat low dimensional systems: Difference between revisions
| Line 114: | Line 114: | ||
Create the input file: | Create the input file: | ||
$ yambo -F yambo_cut2D.in -r -J 2D | $ yambo -F yambo_cut2D.in -r -J 2D | ||
Revision as of 08:51, 31 March 2017
In this tutorial you will learn how to treat low-dimensional material. A small k-sampling is used to reduce the computational cost/time. Later on you can repeat this tutorial but using denser k-grids to check the convergence.
Prerequisites
SAVEfolder for 2D hBN generated with a 6x6x1 k-gridyamboexecutableyppexecutablegnuplot, for plotting spectra- Have Completed the How to obtain an optical spectrum - a guide through the workflow of calculations tutorial
Avoid numerical divergences using the Random Integration Method (RIM)
In DFT runs of low-dimensional materials low dimensional k-grids are generally used. (i.e. NxNx1 for a 2D sheet perpendicular to the z direction) This can create numerical problems in the convergence of the many-body results due to the divergence at small q of the coulomb potential (which appears in all the main equations, see i.e. the exchange self-energy equation).
To eliminate this problem YAMBO uses the so-called Random Integration Method which means to use a Monte Carlo Integration with Random Q-points whose number RandQpts is given in input.
Create the input to generate the ndb.RIM database
$ yambo -F yambo_RIM.in -r
and change the following variable
RandQpts = 1000000 # [RIM] Number of random q-points in the BZ RandGvec = 100 RL # [RIM] Coulomb interaction RS components
N.B RandGvec=100 means to use the RIM for the first 100 G-components of the coulomb potential (Suggestion : later you can check convergence of the HF gap changing these two values) Close input and Run yambo
$ yambo -F yambo_RIM.in -J 2D
At the end you find a new database ndb.RIM and a new report file r-2D_rim_cut. Open it and look inside
[04.02] RIM integrals
=====================
Gamma point sphere radius [au]: 0.08028
Points outside the sphere : 800231
[Int_sBZ(q=0) 1/q^2]*(Vol_sBZ)^(-1/3) = 7.667102
should be < 7.795600
[WR./2D//ndb.RIM]-------------------------------------------
Brillouin Zone Q/K grids (IBZ/BZ): 7 36 7 36
Coulombian RL components : 209
Coulombian diagonal components :yes
RIM random points : 1000000
RIM RL volume [a.u.]: 0.390129
Real RL volume [a.u.]: 0.390112
Eps^-1 reference component :0
Eps^-1 components : 0.00 0.00 0.00
RIM anysotropy factor : 0.000000
- S/N 005962 -------------------------- v.04.01.02 r.00120 -
Summary of Coulomb integrals for non-metallic bands |Q|[au] RIM/Bare:
Q [1]:0.1000E-40.9835 * Q [2]: 0.256404 1.093779
Q [5]: 0.444104 1.031700 * Q [3]: 0.512807 1.023425
Q [6]: 0.678380 1.013439 * Q [4]: 0.769211 1.010447
Q [7]: 0.888208 1.007869
The RIM and Real RL Volumes are quite similar so one million random q-points seems a reasonable number, but again you are invited, later on, to check the convergence of one of the main observables (i.e. HF gap, GW gap, spectrum) changing this number.
Close the report file and perform a calculation of the exchange self-energy to estimate the HF gap using the RIM. Generate the input
$ yambo -F yambo_HF.in -r -x -J 2D
In order to calculate the HF gap only for the last k-point, change the last line as
%[Variables#QPkrange|QPkrange]] # [GW] QP generalized Kpoint/Band indices 7| 7| 4| 5|
Close the input and run yambo
$ yambo -F yambo_HF.in -J 2D
At the end you will find the report file r-2D_HF_and_locXC_rim_cut and the output file o-2D.hf. Open them and have a look
# K-point Band Eo Ehf DFT HF 7.00000 4.00000 0.00000 -3.21640 -16.21949 -19.43589 7.00000 5.00000 4.40109 9.68783 -11.10752 -5.82078
The HF gap is 12.91 eV obtained subtracting the 2 values in the fourth column Doing a similar HF calculation without generating and reading the RIM database the HF gap results to be 12.69 eV. Indeed the presence of the numerical instability is evident only using denser k-grids with respect to the one used in this Tutorial (6x6x1) Suggestion: later you can generate other SAVE directories with denser k-grids and check the HF gap. The results of the HF gap calculated with different k-grids without (noRIM) and with Random Inetgration Method (RIM) to show up the problem are reported:
noRIM RIM 6x6x1 12.69eV 12.91eV 12x12x1 12.80eV 12.89eV 15x15x1 12.96eV 12.90eV 45x45x1 15.52eV 12.96eV
So the home message is : use always the RIM in MB simulations of low-dimensional materials. Before start the next section please enter in the 2D directory and delete ndb.HF_and_locXC.
Generate a truncated coulomb potential
To simulate an isolated nano-material a convergence with cell vacuum size is in principle required, like in the DFT runs. The use of a truncated Coulomb potential allows to achieve faster convergence eliminating the interaction between the repeated images along the non-periodic direction (see i.e. D. Varsano et al Phys. Rev. B and .. ) In this tutorial we learn how to generate a box-like cutoff for a 2D system with the non-periodic direction along z.
In YAMBO you can use :
- spherical cutoff (for 0D systems)
- cylindrical cutoff (for 1D systems)
- box-like cutoff (for 0D, 1D and 2D systems)
The Coulomb potential with a box-like cutoff is defined as
Then the FT component is
where
For a 2D-system with non period direction along z-axis we have
Important remarks:
- the Random Integration Method (RIM) is required to perform the Q-space integration
- for sufficiently large supercells a choose L_i slightly smaller than the cell size in the i-direction ensures to avoid interaction between replicas
Create the input file:
$ yambo -F yambo_cut2D.in -r -J 2D
Change the following variables as:
CUTGeo = "box z" # [CUT] Coulomb Cutoff geometry: box/cylinder/sphere X/Y/Z/XY.. % CUTBox 0.00 | 0.00 | 32.0 | # [CUT] [au] Box sides
Close the input file and run yambo:
$ yambo -F yambo_cut2D.in -J 2D
in the directory 2D you will find a new database ndb.cutoff
Use the truncated coulomb potential in a G0W0-PPA calculation
Generate the input reading ndb.RIM and ndb.cutoff previously generated:
$ yambo -J 2D -F yambo_G0W0.in -p p -g n -r -k hartree -V qp In the input change the following variables EXXRLvcs = 40 Ry # [XX] Exchange RL components NGsBlkXp = 4 Ry # [Xp] Response block size BndsRnXp 1 | 40 | # [Xp] Polarization function bands QPkrange # [GW] QP generalized Kpoint/Band indices 7| 7| 4| 5|
Close the input and run yambo
$ yambo -F yambo_G0W0.in -J 2D
At the end you find a new report file r-2D_em1d_ppa_HF_and_locXC_gw0_rim_cut. As usual open it and have a look. and also a new output file o-2D.qp. The G0W0 gap is now 4.40 eV (LDA) + 3.72 eV (G0W0 correction) = 8.12 eV As you have learned in the previous tutorials the correlation part of the self-energy strongly reduces the HF gap.
Use the truncated coulomb potential in a BSE calculation
Generate the input for the BSE calculation.
$ yambo -J 2D -F yambo_BSE.in -r -o b -p p -y d -k sex -V all
With -V all the largest verbosity is activated and a long input file is generated and only few variables need to be changed.
Note with -J 2D -p p we read the static part of the screening matrix from the ndb.pp database
Put the number of G-vectors in the exchange and correlation part of the kernel like in the h-BN bulk
BSENGexx= 40 Ry # [BSK] Exchange components BSENGBlk= 4 Ry # [BSK] Screened interaction block size
use the simple rigid scissor for the QP energies
% KfnQP_E 3.72000000 | 1.000000 | 1.000000 | # [EXTQP BSK BSS] E parameters (c/v) eV|adim|adim
Set the number of bands involved in the BSE matrix
% BSEBands 2 | 6 | # [BSK] Bands range
Increase the number of energy steps
BEnSteps= 500 # [BSS] Energy steps
To write excitonic WFs for Post-processing, uncomment the following line
#WRbsWF # [BSS] Write to disk excitonic the WFs
Close the input file and run yambo
$ yambo -J 2D -F yambo_BSE.in
Look at the report file r-2D_optics_bse_bsk_bss_em1d_ppa_rim_cut and use gnuplot to plot o-2D.eps_q1_diago_bse
Analyze the differences with corresponding GW and BSE calculations without the use of a truncated coulomb potential
Generate the ndb.RIM in a new directory 2D_NC
$ yambo -J 2D_NC -F yambo_RIM.in
Open the input file yambo_G0W0.in and set back CUTGeo= "none"
Close the input and run yambo
$ yambo -J 2D_NC -F yambo_G0W0.in
You will find a new report r-2D_NC_optics_bse_bsk_bss_em1d_ppa_rim_cut. You are invited to see the difference with the previous one r-2D_optics_bse_bsk_bss_em1d_ppa_rim_cut
and also a new output file o-2D_NC.qp is present. Open and check the QP correction this time A value of 2.81 instead of 3.72 eV is obtained
Are you able to explain this result?
Now redoo the BSE calculation but without cutoff.
Open the yambo_BSE.in and put CUTGeo= "none"
and set the QP correction obtained without cutoff
% KfnQP_E 2.830000 | 1.000000 | 1.000000 | # [EXTQP BSK BSS] E parameters (c/v) eV|adim|adim
Close the input file and run yambo
$ yambo -J 2D_NC -F yambo_BSE.in
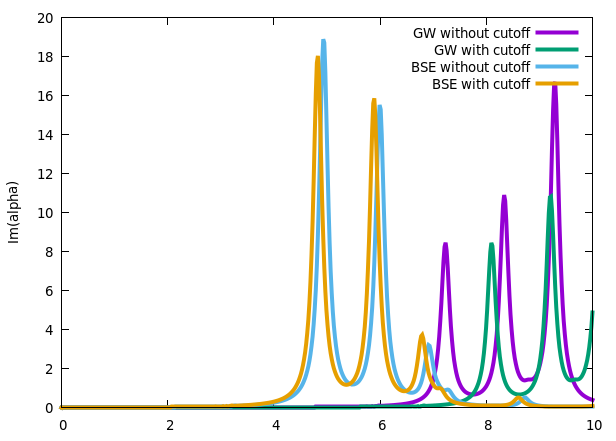
Plot the dielectric functions
$ gnuplot gnuplot> plot 'o-2D_NC.eps_q1_diago_bse' u 1:4 w l title 'GW without cutoff' ,'o-2D.eps_q1_diago_bse' u 1:4 w l title ' GW with cutoff' gnuplot> replot 'o-2D_NC.eps_q1_diago_bse' u 1:2 w l title 'BSE without cutoff' ,'o-2D.eps_q1_diago_bse' u 1:2 w l title 'BSE with cutoff'
You will see