Real time approach to non-linear response (SHG)
Second Harmonic Generation in AlAs
In this tutorial, we will calculate the second harmonic generation of bulk AlAs, the Yambo databases can be downloaded here: AlAs_DBs.tar.gz (10 MB). The first steps of this tutorials are the same as the one on Prerequisites for Real-Time propagation with Yambo with the only difference that we will work on AlAs and we will consider an external field in the direction 1.000000 | 1.000000 | 0.000000 |. The DFT input are available here: ABINIT or QuantumEspresso.
You can run the DFT calculation with ABINIT with the command:
abinit < AlAs.in > output_AlAs
or using QuantumEspresso:
pw.x -inp AlAs.scf.in > output_scf pw.x -inp AlAs.nscf.in > output_scf
and then import the ABINIT wave-function with the command:
a2y -F AlAso_DS2_WFK.nc
and the QuantumEspresso one, in the folder AlAs.save with the command:
p2y
Now we consider an external field in the [1,1,0] direction and remove symmetries not compatible with this field, as explained in the tutorial Prerequisites for Real-Time propagation with Yambo.
Real-time simulation for the SHG
You can generate the input file with the command yambo_nl -u n:
nloptics # [R NL] Non-linear optics % NLBands 3 | 6 | # [NL] Bands % NLstep= 0.0100 fs # [NL] Real Time step length NLverbosity= "high" # [NL] Verbosity level (low | high) NLtime=-1.000000 fs # [NL] Simulation Time NLintegrator= "INVINT" # [NL] Integrator ("EULEREXP/RK4/RK2EXP/HEUN/INVINT/CRANKNIC") NLCorrelation= "IPA" # [NL] Correlation ("IPA/HARTREE/TDDFT/LRC/JGM/SEX/HF") NLLrcAlpha= 0.000000 # [NL] Long Range Correction % NLEnRange 1.000000 | 5.000000 | eV # [NL] Energy range % NLEnSteps= 5 # [NL] Energy steps NLDamping= 0.150000 eV # [NL] Damping % Field1_Dir 1.000000 | 1.000000 | 0.000000 | # [RT Field1] Versor Field1_kind= "SOFTSIN" # [NL ExtF] Kind(SIN|SOFTSIN|RES|ANTIRES|GAUSS|DELTA|QSSIN)
The line |1.000000 | 1.000000 | 0.000000 | # [RT Field1] Versor referees to the direction of the external field (x,y,0). At present only an external field is present but the code can be easily generalized to deal with more fields.
The default parameters of Yambo/Lumen are already tuned for second-harmonic generation, so the only thing you have to change is the band range, between 3 and 6 and the energy range between 1.0-5.0 eV and the number of energy steps in this interval that we set to 10. Notice that you cannot set to zero the lowest value of the energy range because this will requires a simulation that lasts infinite time, see below. Finally, consider that Yambo performs a separate calculation for each frequency, so if you set many energy steps the computational time grows linearly with this number.
Notice that we set NLverbosity= "high" in this way the code will produce a file for each laser frequency containing the time dependent polarization.
Run yambo_nl. Calculations will take about fifteen minutes on a single processor PC, you have time to study the next section that explains how non-linear response is extracted from the real-time simulations.
In order to speed up calculations, you can run them in parallel.
Non-linear response with Yambo
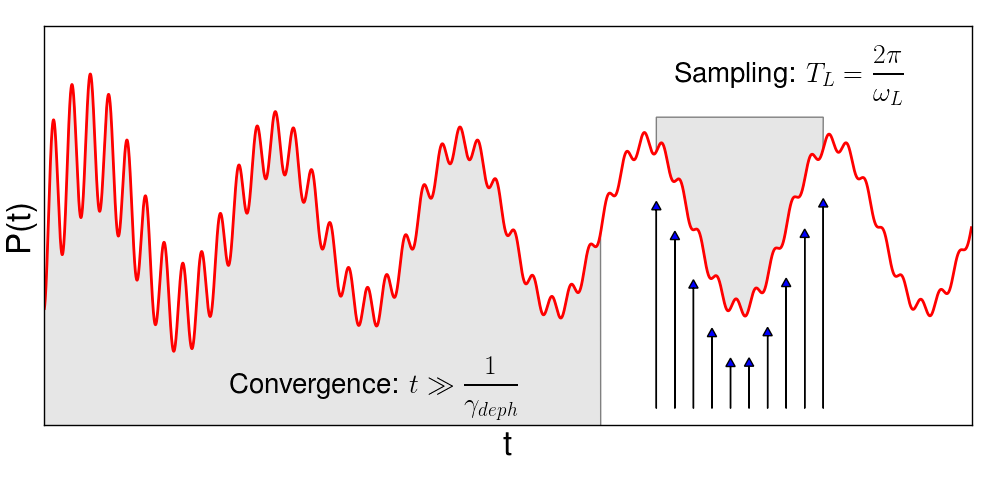
In order to calculate the non-linear response, the system is excited with different laser fields with a sinusoidal shape at frequencies [math]\displaystyle{ \omega_1, \omega_2, .... , \omega_n }[/math] determined by the parameters NLEnRange and NLEnSteps. A dephasing term is added to the Hamiltonian [math]\displaystyle{ \gamma = }[/math]NLDamping to simulate a finite broadening and to remove the eigenmodes that are excited by the sudden turning on of the external field. After the dephasing time the outgoing signal is analyzed to extract the non-linear coefficients as shown in the figure below:
In the report file r_nlinear you will find the length of the dephasing part and of the sampling one:
Dephasing Time [fs]: 52.65695 Sampling Time [fs]: 4.18566 Total simulation time [fs]: 56.84262
The length of the dephasing interval is inversely proportional to the damping term [math]\displaystyle{ T_{depth} \simeq 1/\gamma }[/math] while the length of the sampling is dictated by the smallest frequency we are interested in: [math]\displaystyle{ T_{samp} \simeq 1/\omega_1 }[/math]. For this reason if [math]\displaystyle{ \omega_1=0 }[/math] or [math]\displaystyle{ \gamma = 0 }[/math] simulation time goes to infinity. The response at zero frequency can be calculated as limit of small frequency perturbation.
You can have a look to the file src/nloptics/NL_initialize.F to see how simulation lengths are defined.
Calculations can take some time, run them in parallel, the best number of processors = number of frequencies or reduce the number of frequencies step in the SHG.
Analysis of the results
In the sampling region we suppose that the polarization can be written as: [math]\displaystyle{ \bf{P}(t) = \sum_{n=-\infty}^{+\infty} \bf{p}_n e^{-i\omega_n t} }[/math] where the coefficient [math]\displaystyle{ \bf{p}_1,...,\bf{p}_n }[/math] are related to [math]\displaystyle{ \chi^{(1)},...,\chi^{(n)} }[/math]. We sample the polarization signal at different times and invert the previous equation by truncating the sum at a finite order [1].
This is done with the command ypp_nl -u that automatically produce an input with the correct values:
nonlinear # [R] NonLinear Optics Post-Processing
Xorder= 4 # Max order of the response functions
% TimeRange
52.65695 | -1.00000 | fs # Time-window where processing is done
%
ETStpsRt= 200 # Total Energy steps
% EnRngeRt
0.00000 | 10.00000 | eV # Energy range
%
DampMode= "NONE" # Damping type ( NONE | LORENTZIAN | GAUSSIAN )
DampFactor= 0.10000 eV # Damping parameter
where Xorder is the order where the previous sum is truncated, and the TimeRange specifies the sampling region. Notice that differently from the first tutorial, in this case, we do not need Damping in ypp_nl because we already included it in the real-time dynamics. Run ypp_nl and it will produce a file called o.YPP-X_probe_order_2. This file contains the different components of [math]\displaystyle{ \chi^2_{xy*} }[/math] and in particular the columns 6 and 7 correspond to the imaginary and real part of [math]\displaystyle{ \chi^2_{xyz} }[/math]. You can plot the result with gnuplot and the command:
p 'o.YPP-X_probe_order_2' u 1:(sqrt($6**2+$7**2)) w lp ps 1.5 pt 7 lw 1.5
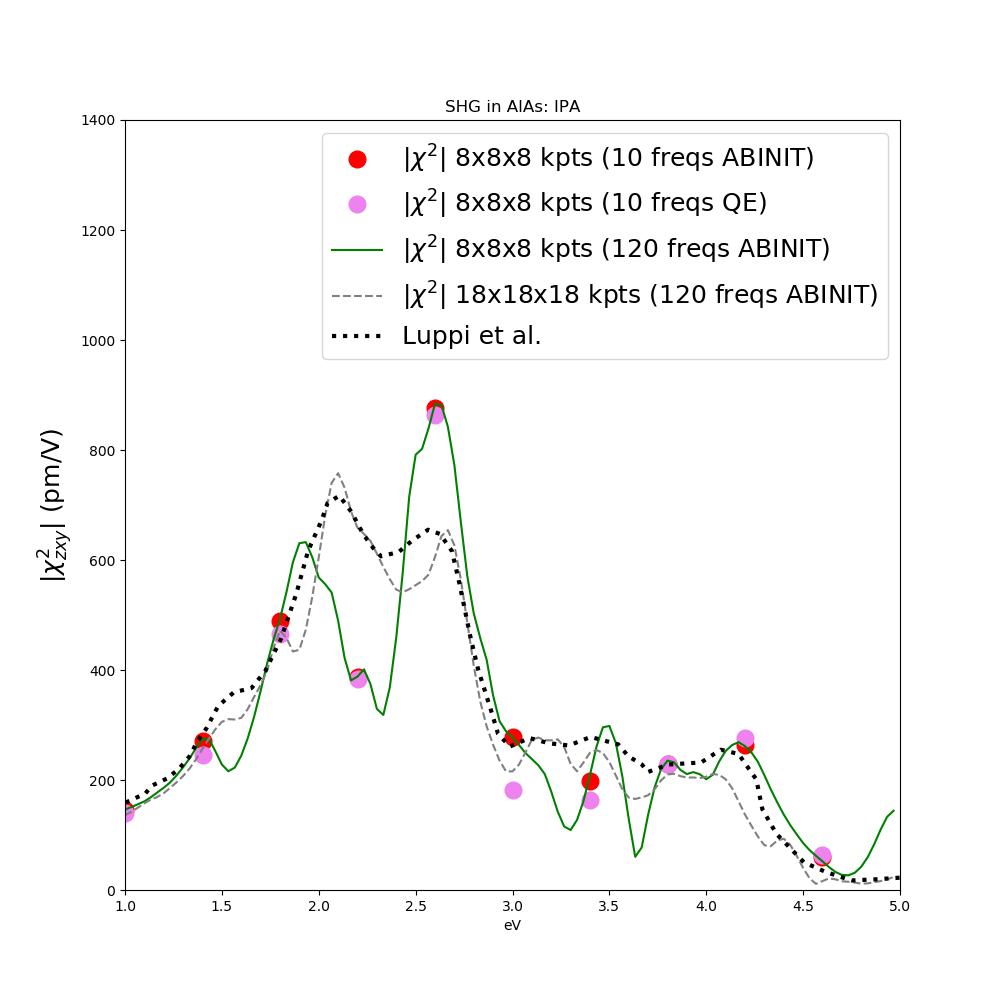
the result should look like
and compare it with the [math]\displaystyle{ \chi^2_{zxy} }[/math] calculated with more frequencies and with the converged result on a [math]\displaystyle{ 18x18x18 }[/math] k-point grid and bands between 2 and 10. In the figure you can find also the comparison with the results of Ref. [2]. Notice that the QuantumEspresso results are slightly different from the Abinit ones. This is due to the different pseudo-potential employed in the calculations if pseudopotentials were the same calculation would have been identical. You can download the script to generate this plot and the converged results here.
Notice that : the following parameters are not used in the non-linear response analysis: EnRngeRt, ETStpsRt, DampMode, DampFactor. The damping factor is set directly in the real-time simulation.
System of units in Non-linear Optics: notice that in Yambo the non-linear response functions are in the gaussian system of units, for example the [math]\displaystyle{ \chi^2 (\omega) }[/math] is in cm/statvolt. In order to convert the non-linear coefficients between different system of units, you can have a look at the Appendix C of the book "Non-linear optics" by Robert W. Boyd.
More tutorials on non-linear response (Third harmonic generation, parallelization, spin-orbit etc..) with Yambo can be found here: More Tutorials.
Analysis of the results using YamboPy
The analysis of the result performed in the previous section using ypp_nl can be performed using python script YamboPy.
In YamboPy we implemented all necessary functions to reads the Yambo databases and post-process the results. Here we show how to get the SHG signal from the previous
simulations. We suppose you correctly installed YamboPy on your PC. Go in the folder where you ran non-linear calculation and type in the python:
from yambopy import * NLDB=YamboNLDB() pol =NLDB.Polarization[0] time=NLDB.IO_TIME_points
in this way you read all the Non-linear databases. If your runs are in a different folder then the 'SAVE' one you can specify it using the command:
NLDB=YamboNLDB(calc='MYJOB')
now in the array pol you have all the polarization for all laser frequencies in the three Cartesian directions, while the variable time contains all the time series of your simulation.
Now you can get the non-linear response with the command:
Harmonic_Analysis(NLDB,X_order=4)
this command will perform a Fourier analysis of the results in the same way of ypp_nl and generate new files with all the requested harmonics o.YamboPy-X_probe_order_1, o.YamboPy-X_probe_order_2 etc...
equivalent to the one generated by ypp_nl. Results can be plot with gnuplot using the command:
p 'o.YamboPy-X_probe_order_2' u 1:(sqrt($6**2+$7**2)) w lp ps 1.5 pt 7 lw 1.5
The script that performs non-linear analysis can be found in yambopy/nl/harmonic_analysis.py.
We strongly advice you to have a look to this script and modify it according
to your needs and in order to extract other non-linear response functions.
How to choose the external field direction for the different X2
In the X2abc response you have three field directions. The two components b and c are determined by the external field and the third a
is the direction where you measure the response.
The external field in Yambo is set using the variable
% Field1_Dir 1.000000 | 0.000000 | 0.000000 | # [NL ExtF] Versor . %
For example if you set in Yambo field direction as:
1.0 | 0.0 | 0.0 | ---> you calculate all components X2*xx 0.0 | 1.0 | 0.0 | ---> you calculate all components X2*yy 0.0 | 0.0 | 1.0 | ---> you calculate all components X2*zz
the * correspond to the different direction in the response file o.YPP-X_probe_order_2.
In the o.YPP-X_probe_order_2 you have seven columns:
The first column is the energy omega, the 2nd and 3rd columns are the imaginary and real part of X2x** the 4th and 5th columns are the imaginary and real part of X2y** the 6th and 7th columns are the imaginary and real part of X2z**
where the ** are the direction of the incoming field, see above.
For example if you want to calculate the [math]\displaystyle{ \chi^{(2)}_{zxx} }[/math] you put the external field in the direction 1.0 | 0.0 | 0.0 |
and then plot the column 6 and 7 of the o.YPP-X_probe_order_2 file.
In order to get the other components of the X2 the calculation are more involved. For example if you put field in the
1.0 | 1.0 | 0.0 |
this corresponds to [math]\displaystyle{ E(t)=\frac{1}{\sqrt{2}} [ E_x(t) + E_y(t) ] }[/math] and so at the second order you will have [math]\displaystyle{ E^2(t)=\frac{1}{2} \left [ E^2_x(t) + E^2_y(t) + E_x(t) E_y(t) + E_y(t) E_x(t) \right] }[/math]
this means that the X2 in the o.YPP-X_probe_order_2 will correspond to a linear combination of the following different response functions.
For example in the the 2nd and 3rd columns are the imaginary and real part of:
[math]\displaystyle{ \chi^{(2)}_{x**}=\frac{1}{2} \left [\chi^2_{xxx}+\chi^{(2)}_{xyy} + \chi^{(2)}_{xxy} + \chi^{(2)}_{xyx} \right ] }[/math]
the same for the other column replacing the first x for y,z.
If you know that some components are zero this allow you to extract the corresponding off-diagonal part of [math]\displaystyle{ \chi^{(2)}_{abc} }[/math] otherwise you have to perform different calculations to get the component you are interested in.
Now we present a simple example of monolayer hBN (m-hBN).
In m-hBN there is only a non-zero component of the [math]\displaystyle{ \chi^{(2)} }[/math]and all the others are related by symmetry:
[math]\displaystyle{ \chi^{(2)}_{yyy}=-\chi^{(2)}_{yxx}=-\chi^{(2)}_{xxy}=-\chi^{(2)}_{xyx} }[/math]
so if you put the field in the |1|1|0| direction you will get:
[math]\displaystyle{ \chi^{(2)}_{x**} = \frac{1}{2} \left[\chi^{(2)}_{xxy} + \chi^{(2)}_{xyx} \right] = - \chi^{(2)}_{yyy} }[/math]
[math]\displaystyle{ \chi^{(2)}_{y**} =\frac{1}{2} \left[ \chi^{(2)}_{yyy} + \chi^{(2)}_{yxx} \right] = 0.0 }[/math]
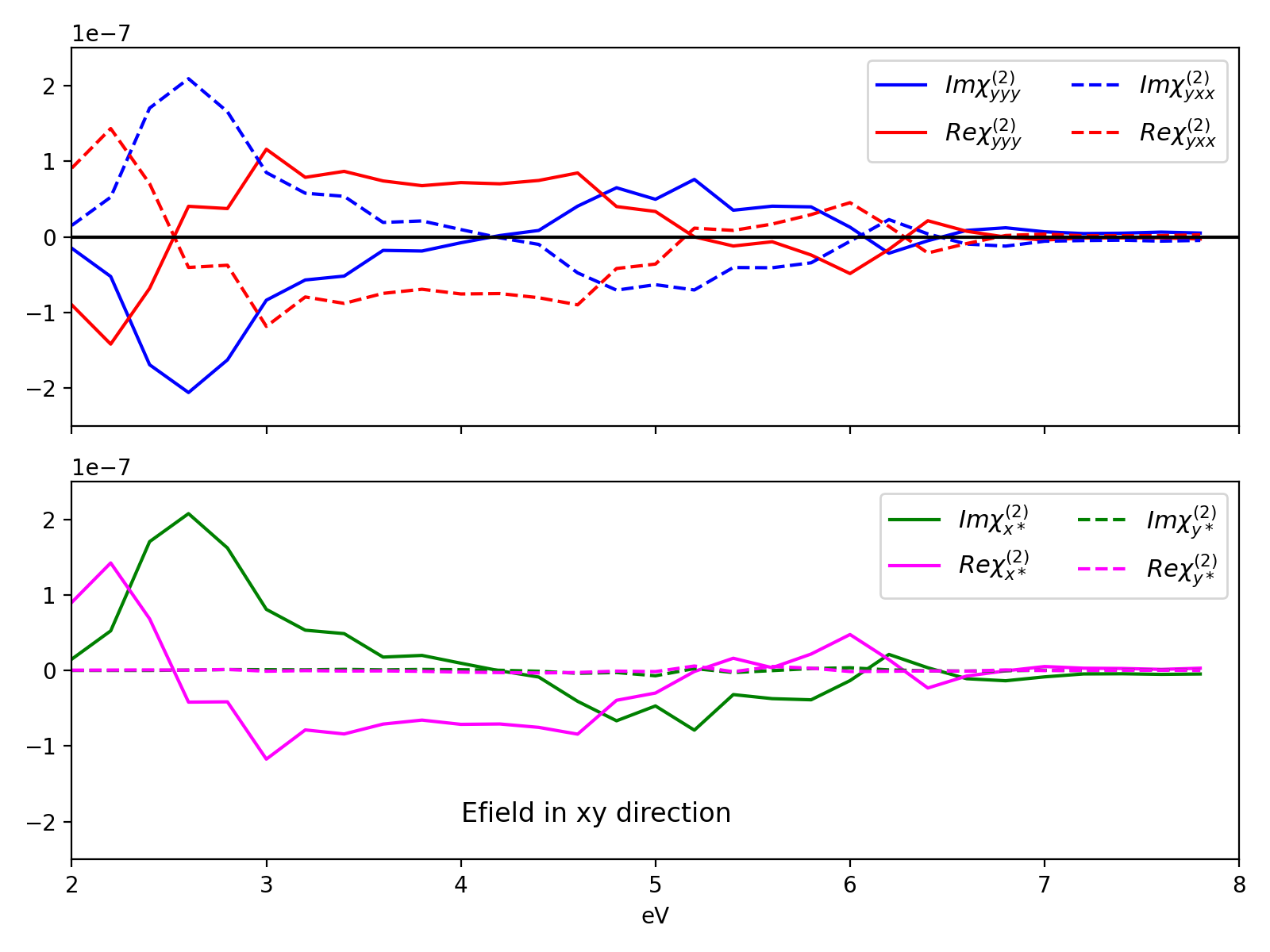
In the figure below you can see the different [math]\displaystyle{ \chi^{(2)} }[/math] of monolayer hBN.
as you can see in the second panel, when the field is in the xy you get a linear combination of [math]\displaystyle{ \chi^{(2)} }[/math] corresponding to the equation above, in this case the y is zero while the x component is equal to [math]\displaystyle{ -\chi^{(2)}_{yyy} }[/math].
Nota bene: if you change the direction of the external field you must to remove the corresponding symmetries as explained in the tutorial Prerequisites for Real Time_propagation with Yambo#Reduce symmetries real-time linear response tutorial. If you have to calculate [math]\displaystyle{ \chi^{(2)} }[/math] along many directions it can be convenient to remove all symmetries at once.
Non-linear response of low-dimensional structures: 2D or 1D
The Yambo code is a 3D periodic code, so when you want to study a low-dimensional system 2D or 1D, you have to use a supercell approach. For example to simulate the non-linear response in a 2D-crystal one, can put the crystal in the xy plane and choose a larger distance in the z-direction in order to reduce the interaction between the periodic replica. Clearly in this case k-point sampling will be only in the x,y directions. For calculations on this type of systems, these two warnings must be taken into account:
- if you calculate GW corrections or include electron-hole interaction in the linear/non-linear response it is a good idea to use a Coulomb cutoff, similar to the 2D BSE case How to treat low dimensional systems. You can add the cutoff just adding the "-r" in the input generation.
- the calculation of SHG and THG are always performed respect to the supercell, therefore you have to re-scale the result to the effective thickness of the layer, usually the inter-layer distance of the corresponding bulk material for 2D systems: [math]\displaystyle{ \chi_{rescaled}(\omega) = L_z/d_{eff} \cdot \chi(\omega) }[/math] where [math]\displaystyle{ L_z }[/math] is the z-dimension of the supercell, and [math]\displaystyle{ d_{eff} }[/math] is the effective thickness of the 2D system.
Nota bene: Non-linear response along non-periodic directions is not implemented in Yambo, the code will print zero in these directions for all response functions. We plan to implement it in a future version of the code.
References
- ↑ Nonlinear optics from an ab initio approach by means of the dynamical Berry phase: Application to second- and third-harmonic generation in semiconductors, C. Attaccalite and M. Grüning, Phys. Rev. B 88, 235113(2013)
- ↑ Luppi et al. PRB B, 82, 235201(2010)
Links for schools
- Back to Rome 2023#Tutorials
- Back to ICTP2020
| Prev: Linear response from real time simulations | Now: ICTP Tutorials --> Non Linear Response | Next: Correlation effects in the non-linear response |